Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

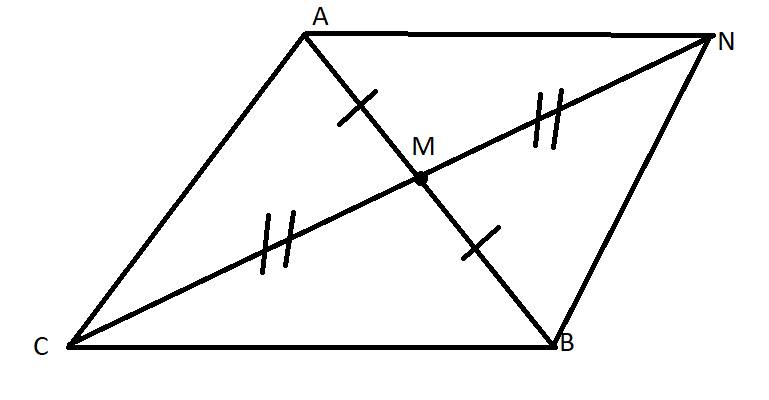
a, Xét ΔAMN và ΔBMC:
AM=BM(M là trung điểm của AB)
MC=MN(GT)
\(\widehat{AMN}=\widehat{BMC}\) (hai góc đối đỉnh)
=>ΔAMN=ΔBMC(c.g.c)
b, ΔAMN=ΔBMC=>\(\widehat{ANM}=\widehat{MCB}\) (2 góc tương ứng) mà 2 góc này nằm ở vị trí so le trong
=>AN//BC
c,+) ΔAMN=ΔBMC =>AN=BC(cạnh tương ứng)
+)Xét ΔAMC và ΔNMB
AM=BM(M là trung điểm của AB)
MC=MN(GT)
\(\widehat{AMC}=\widehat{NMB}\)
=>ΔAMC=ΔNMB(c.g.c)=>AC=BN(cạnh tương ứng)
+)Xét ΔNAC và ΔCBN
AC=BN(CMT)
AN=BC(CMT)
CN là cạnh chung
=>ΔNAC=ΔCBN(c.c.c)

a) Xét \(\Delta BACvà\Delta NAMcó\)
\(\widehat{BAC}=\widehat{NAM}\) ( đối đỉnh )
\(BA=NA\) ( gt )
\(CA=MA\) ( gt )
\(\Rightarrow\Delta BAC=\Delta NAM\) ( c.g.c )
\(\Rightarrow BC=MN\) ( 2 cạnh tương ứng )
mik chỉ lm đc v hoi xin lũi bn do chx hiểu cái ý 2 câu a

a) Xét Δ AMN và Δ BMC có:
+ MN = MC (gt).
+ \(\widehat{AMN} = \widehat{BMC}\) (2 góc đối đỉnh).
+ MA + MB (M là trung điểm của AB).
\(\Rightarrow\) Δ AMN = Δ BMC (c - g - c).
\(\Rightarrow\) \(\widehat{MAN} = \widehat{MBC}\) (2 góc tương ứng).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) AN // BC (dhnb).
b) Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ E là trung điểm của AC (gt).
\(\Rightarrow\) ME là đường trung bình.
\(\Rightarrow\) ME // BC và ME = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác NBA có:
+ M là trung điểm của AB (gt).
+ F là trung điểm của BN (gt).
\(\Rightarrow\) MF là đường trung bình.
\(\Rightarrow\) MF // BC và MF = \(\dfrac{1}{2}\) BC (Tính chất đường trung bình trong tam giác). (2)
Từ (1) và (2) \(\Rightarrow\) 3 điểm E, M, F thẳng hàng và MF = ME (cùng = \(\dfrac{1}{2}\) BC).
\(\Rightarrow\) M là trung điểm của EF (đpcm).

Ap dụng định lý Pytago vào tam giác vuông \(ABC\)ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=3^2+4^2=25\)
\(\Leftrightarrow\)\(BC=\sqrt{25}=5\)

a) Xét tam giác AMN và tam giác BMC, ta có:
MA = MB (M là trung điểm của AB)
góc NMA = góc BMC (đối đỉnh)
MN = MC (gt)
=> tam giác AMN = tam giác BMC
b) Xét tứ giác ACBN, ta có:
M là trung điểm của AB (gt)
M là trung điểm của CN (MC = MN)
=> Tứ giác ACBN là hình bình hành
=> AN // BC
c) Do tứ giác ACBN là hình bình hành => AN // BC và AN = BC => góc ANC = góc BCN và AN = BC
Xét tam giác NAC và tam giác CBN, ta có:
AN = BC (cmt)
góc ANC = góc BCN (cmt)
CN chung
=> tam giác NAC = tam giác CBN

A B C M N F E
a) Xét \(\Delta BNM\)và \(\Delta ACM\)có :
NM = MC ( gt )
\(\widehat{NMB}=\widehat{CMA}\)( hai góc đối đỉnh )
MB = MA ( gt )
Suy ra : \(\Delta BNM\)= \(\Delta ACM\)( c.g.c )
\(\Rightarrow NB=AC\)( hai cạnh tương ứng )
\(\Rightarrow\widehat{BNM}=\widehat{ACM}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong nên NB // AC
b) Xét \(\Delta BNC\)có \(\widehat{EBC}\)là góc ngoài nên \(\widehat{EBC}\)= \(\widehat{BNC}+\widehat{BCN}\)hay \(\widehat{EBC}\)= \(\widehat{ACM}+\widehat{BCN}=\widehat{ACB}\)
Xét \(\Delta BEC\)và \(\Delta BAC\)có :
BE = AC ( vì NB = BE = AC )
\(\widehat{EBC}\)= \(\widehat{ACB}\)( cmt )
BC ( cạnh chung )
Suy ra : \(\Delta BEC\)= \(\Delta BAC\)( c.g.c )
\(\Rightarrow AB=EC\)( hai cạnh tương ứng )
c) Vì \(\widehat{EFC}=\widehat{AFB}\)( hai góc đối đỉnh )
Mà \(\widehat{AFB}=180^o-\widehat{AFC}\)
\(\Rightarrow\widehat{EFC}+\widehat{AFC}=180^o-\widehat{AFC}+\widehat{AFC}=180^o\)
\(\Rightarrow\widehat{AFE}\)là góc bẹt nên A,F,E thẳng hàng

a: Xét tứ giác ABCQ có
N là trung điểm của AC
N là trung điểm của BQ
Do đó: ABCQ là hình bình hành
Suy ra: AQ//BC và AQ=BC
Xét tứ giác ACBP có
M là trung điểm của AB
M là trung điểm của CP
Do đó: ACBP là hình bình hành
Suy ra: AP//BC và AP=BC
Ta có: AQ//BC
AP//BC
mà AQ,AP có điểm chung là A
nên Q,A,P thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MN=PQ/4
=>PQ=4MN
Có nhầm đề ko z bn ?
ko đâu ko có chuyện nhầm đâu