Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABD và ΔACD có:
AD chung
góc ABD=góc ACD ( do AD là phân giác của góc BAC)
AB=AC ( ΔABC cân tại A)
Do đó:ΔABD=ΔACD (c-g-c) (đpcm)
Ta có:
AD vuông góc BC(tính chất Δ vuông)
EH vuông góc BC (theo đầu bài)
=>AD//EH (cùng vuông góc với BC)
=>góc ADE=góc DEH (2 góc so le trong)
Lại có:ΔDEC cân theo câu c:
=>góc EDC=góc ECD
mà góc ECD=góc ABD (ΔABC cân tại A)
=>góc EDC=góc ABD.
Xét ΔBAD có: góc ABD + góc BAD=90 độ (do ΔBAD vuông tại D)
và ΔDEH có: góc EDH + góc DEH =90 độ (do ΔDEH vuông tại H)
=> góc BAD=góc DEH
Mà góc BAD=góc DAE (AD là phân giác của góc A)
góc ADE=góc DEH (2 góc so le trong)
=>góc DAE=góc ADE
=>ΔAED cân tại E
=>DE=AE
mà DE=EC (ΔDEC cân tại E)
=>AE=EC
=>E là trung điểm của AC
=>3 điểm B,G,E thẳng hàng (đpcm)

a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
b) Ta có: ΔABD=ΔACD(cmt)
nên BD=CD(hai cạnh tương ứng)
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
c) Ta có: ΔABD=ΔACD(cmt)
nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
Xét ΔADC có
H là trung điểm của CD(gt)
HE//AD(cùng vuông góc với BC)
Do đó: E là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Ta có: ΔADC vuông tại D(cmt)
mà DE là đường trung tuyến ứng với cạnh huyền AC(E là trung điểm của AC)
nên \(DE=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay DE=EC
Xét ΔDEC có ED=EC(cmt)
nên ΔDEC cân tại E(Định nghĩa tam giác cân)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE và BA=BE
=>ΔADE cân tại D và BD là trung trực của AE
c: AD=DE
DE<DC
=>AD<DC
d: AH vuông góc BC
DE vuông góc BC
=>AH//DE
góc AFD=góc BFH=90 độ-góc DBC
góc ADF=90 độ-góc ABD
mà góc DBC=góc ABD
nên góc AFD=góc ADF
=>ΔADF cân tại A

a: Xét ΔAMC và ΔDMB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)
MC=MB
Do đó: ΔAMC=ΔDMB
Suy ra: AC=DB và \(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//DB
hay DB\(\perp\)AB
Xét ΔCAB vuông tại A và ΔDBA vuông tại D có
BA chung
CA=DB
Do đó: ΔCAB=ΔDBA
Suy ra: CB=DA
b: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Suy ra: AD=10cm

a,
Ta có : D là trung điểm của BC
Mà Δ ABC cân tại A
=> AD là đường cao
=> AD là đường phân giác \(\widehat{BAC}\)
Xét Δ ABD và Δ ACD, có :
\(\widehat{ADB}=\widehat{ADC}=90^o\)
\(\widehat{ABD}=\widehat{ACD}\) (Δ ABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ ABD = Δ ACD (g.g.g)
b, Ta có : AD là đường cao (cmt)
=> AD ⊥ BC
c, Xét Δ AED và Δ AFD, có :
AD là cạnh chung
\(\widehat{AED}=\widehat{AFD}=90^o\)
\(\widehat{EAD}=\widehat{FAD}\) (AD là đường phân giác \(\widehat{BAC}\))
=> Δ AED = Δ AFD (g.c.g)
=> ED = FD
Xét Δ EBD vuông tại E và Δ FCD vuông tại F, có :
ED = FD
DB = DC (D là trung điểm BC)
=> Δ EBD = Δ FCD (ch - cgv)
d, Ta có : BC = 2DC (D là trung điểm BC)
=>12 = 2DC
=> DC = 6 (cm)
Xét Δ ADC vuông tại D, có :
\(AC^2=AD^2+DC^2\) (định lí Py - ta - go)
=> \(10^2=AD^2+6^2\)
=> \(64=AD^2\)
=> AD = 8 (cm)
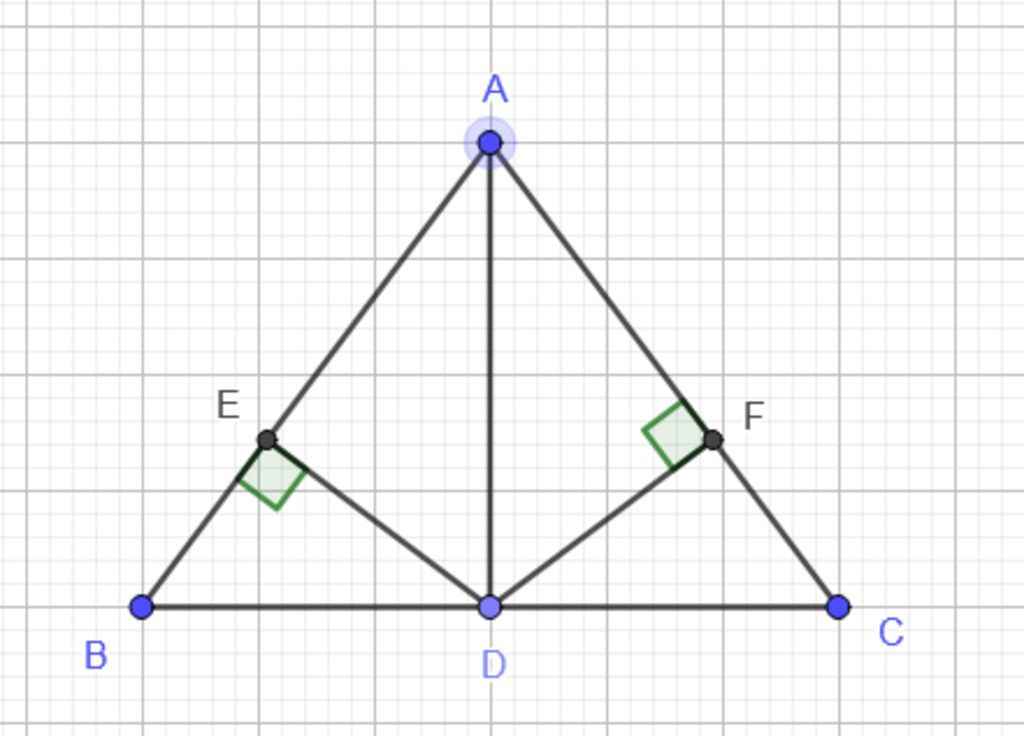

a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
=>ΔABD=ΔACD
b: ΔABC cân tại A
mà AD là trung tuyến
nên AD vuông góc BC
d: DG là đường trung bình
=>DG//AC