Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(1\right)=a_{2017}+a_{2016}+...+a_3+a_2+a_1+a_0\)
\(f\left(-1\right)=-a_{2017}+a_{2016}+...-a_3+a_2-a_1+a_0\)
\(f\left(1\right)+f\left(-1\right)=2\left(a_{2016}+a_{2014}+...+a_2+a_0\right)\)
\(S=\frac{f\left(1\right)+f\left(-1\right)}{2}=\frac{3^{2017}+1}{2}\)

\(f\left(3\right)=a_13^1+a_23^3+a_33^5\)
\(\Rightarrow f\left(-3\right)=-a_13^1+-a_23^3+-a_33^5=-\left(a_13^1+a_23^3+a_33^5\right)=-f\left(3\right)=208\Rightarrow f\left(3\right)=-208\)
Vậy f(3)=-208

a. Ta có: f(x) + h(x) = g(x)
Suy ra: h(x) = g(x) – f(x) = (x4 – x3 + x2 + 5) – (x4 – 3x2 + x – 1)
= x4 – x3 + x2 + 5 – x4 + 3x2 – x + 1
= -x3 + 4x2 – x + 6
b. Ta có: f(x) – h(x) = g(x)
Suy ra: h(x) = f(x) – g(x) = (x4 – 3x2 + x – 1) – (x4 – x3 + x2 + 5)
= x4 – 3x2 + x – 1 – x4 + x3 – x2 – 5
= x3 – 4x2 + x – 6

Lời giải:
Ta có thể viết dạng của $f(x)$ như sau:
\(f(x)=(x-1)(x-2)(x-3)(x-t)+g(x)\)
Trong đó, \(t\) là một số bất kỳ nào đó và \(g(x)\) là đa thức có bậc nhỏ hơn hoặc bằng $3$
Giả sử \(g(x)=mx^3+nx^2+px\)
\(\left\{\begin{matrix} f(1)=g(1)=m+n+p=10\\ f(2)=g(2)=8m+4n+2p=20\\ f(3)=g(3)=27m+9n+3p=30\end{matrix}\right.\)
Giải hệ trên thu được \(m=0,n=0,p=10\)
Như vậy \(f(x)=(x-1)(x-2)(x-3)(x-t)+10x\)
Do đó \(\left\{\begin{matrix} f(12)=990(12-t)+120=12000-990t\\ f(-8)=-990(-8-t)-80=7840+990t\end{matrix}\right.\)
\(\Rightarrow \frac{f(12)+f(-8)}{10}+26=\frac{12000+7840}{10}+26=2010\) (đpcm)

Ta có \(f\left(1\right)=a+b+c\) và \(f\left(-1\right)=a-b+c\)
Vì \(f\left(1\right)=f\left(-1\right)\) nên \(a+b+c=a-b+c\Rightarrow b=0\)
\(f\left(x\right)=ax^2+bx+c=ax^2+c\)
\(f\left(-x\right)=ax^2-bx+c=ax^2+c\)
Vậy \(f\left(x\right)=f\left(-x\right)\)

\(x.f\left(x+2\right)=\left(x^2-9\right).f\left(x\right)\)
+ Thay \(x=3\) vào đa thức \(f\left(x\right)\) ta được:
\(3.f\left(3+2\right)=\left(3^2-9\right).f\left(3\right)\)
\(\Rightarrow3.f\left(5\right)=\left(9-9\right).f\left(3\right)\)
\(\Rightarrow3.f\left(5\right)=0.f\left(3\right)\)
\(\Rightarrow3.f\left(5\right)=0\)
\(\Rightarrow f\left(5\right)=0:3\)
\(\Rightarrow f\left(5\right)=0.\)
Vậy \(x=5\) là nghiệm của đa thức \(f\left(x\right)\) (1).
+ Thay \(x=-3\) vào đa thức \(f\left(x\right)\) ta được:
\(-3.f\left[\left(-3\right)+2\right]=\left[\left(-3\right)^2-9\right].f\left(-3\right)\)
\(\Rightarrow-3.f\left(-1\right)=\left(9-9\right).f\left(-3\right)\)
\(\Rightarrow-3.f\left(-1\right)=0.f\left(-3\right)\)
\(\Rightarrow-3.f\left(-1\right)=0\)
\(\Rightarrow f\left(-1\right)=0:\left(-3\right)\)
\(\Rightarrow f\left(-1\right)=0.\)
Vậy \(x=-1\) là nghiệm của đa thức \(f\left(x\right)\) (2).
+ Thay \(x=0\) vào đa thức \(f\left(x\right)\) ta được:
\(0.f\left(0+2\right)=\left(0^2-9\right).f\left(0\right)\)
\(\Rightarrow0.f\left(2\right)=\left(0-9\right).f\left(0\right)\)
\(\Rightarrow0=-9.f\left(0\right)\)
\(\Rightarrow f\left(0\right)=0:\left(-9\right)\)
\(\Rightarrow f\left(0\right)=0.\)
Vậy \(x=0\) là nghiệm của đa thức \(f\left(x\right)\) (3).
Từ (1), (2) và (3) \(\Rightarrow\) Đa thức \(f\left(x\right)\) có ít nhất 3 nghiệm đó là: \(x=3;x=-3\) và \(x=0\left(đpcm\right).\)
Chúc bạn học tốt!
Tham khảo :
Xét với x=3x=3 thì : 3.f(5)=(32−9).f(3)3.f(5)=(32−9).f(3)
⇒3.f(5)=0⇒f(5)=0⇒3.f(5)=0⇒f(5)=0 (*)
Xét với x=0⇔0=−9.f(0)⇒f(0)=0x=0⇔0=−9.f(0)⇒f(0)=0
nên x=0x=0 là 1 nghiệm của đa thức f(x)f(x) (1)
Xét với x=−3⇔3.f(−1)=0⇒f(−1)=0x=−3⇔3.f(−1)=0⇒f(−1)=0
nên x=−1x=−1 là 1 nghiệm của đa thức f(x)f(x) (2)
Từ (*)(1)(2) ⇒⇒ f(x)f(x) có ít nhất 3 nghiệm.
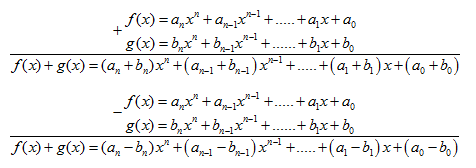
Lời giải:
\(f(1)=f(-1)\)
\(\Leftrightarrow a_4+a_3+a_2+a_1+a_0=a_4-a_3+a_2-a_1+a_0\)
\(\Leftrightarrow 2(a_3+a_1)=0\Leftrightarrow a_3+a_1=0(1)\)
\(f(2)=f(-2)\)
\(\Leftrightarrow 16a_4+8a_3+4a_2+2a_1+a_0=16a_4-8a_3+4a_2-2a_1+a_0\)
\(\Leftrightarrow 16a_3+4a_1=0\Leftrightarrow 4a_3+a_1=0(2)\)
Từ \((1);(2)\Rightarrow a_3=a_1=0\)
Do đó:
\(f(x)=a_4x^4+a_2x^2+a_0\)
\(\Rightarrow f(-x)=a_4(-x)^4+a_2(-x)^2+a_0=a_4x^4+a_2x^2+a_0\)
Vậy $f(x)=f(-x)$.