Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Xét ΔKAN vuông tại K và ΔQAN vuông tại Q có
AN chung
\(\widehat{KAN}=\widehat{QAN}\)
Do đó: ΔKAN=ΔQAN(cạnh huyền-góc nhọn)
Suy ra: AK=AQ(hai cạnh tương ứng)

a) Xét ΔAHB và ΔAHC có
AB=AC(ΔBAC cân tại A)
AH chung
BH=CH(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-c-c)
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay AH\(\perp\)BC tại H
b) Xét ΔADM và ΔBHM có
\(\widehat{DAM}=\widehat{HBM}\)(hai góc so le trong, AD//BH)
MA=MB(M là trung điểm của AB)
\(\widehat{AMD}=\widehat{BMH}\)(hai góc đối đỉnh)
Do đó: ΔADM=ΔBHM(g-c-g)
Suy ra: AD=BH(hai cạnh tương ứng)
mà AD=12cm(gt)
nên BH=12cm
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AH^2=20^2-12^2=256\)
hay AH=16(cm)

a) Diện tích tam giác ABC (Heron)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(AB+BC+AC\right)\left(AB+BC-AC\right)\left(BC+AC-AB\right)\left(AC+AB-BC\right)}\)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(6+10+8\right)\left(6+10-8\right)\left(10+8-6\right)\left(8+6-10\right)}=24\left(cm^2\right)\)
b)Xét tam giác ABC có
\(BC^2=10^2=100\left(cm\right)\)
\(AB^2+AC^2=6^2+8^2=100\left(cm\right)\)
Vì 100cm=100cm
\(\Rightarrow BC^2=AB^2+AC^2\)
=> Tam giác ABC vuông tại A
Xét diện tích tam giác ABC thường \(S_{ABCt}=\frac{AH.BC}{2}\left(1\right)\)
Xét diện tích tam giác ABC vuông \(S_{ABCv}=\frac{AC.AB}{2}\left(2\right)\)
Từ (1) và (2)
\(\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH.10=8.6\Leftrightarrow AH=4,8\left(cm\right)\)
Xét tam giác ABH vuông tại H
\(\Rightarrow BH^2=AB^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}\)
\(\Rightarrow BH=\sqrt{6^2-13,3^2}=3,6\left(cm\right)\)
Xét tam giác ACH vuông tại H
\(\Rightarrow HC^2=AC^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{8^2-4,8^2}=6,4\left(cm\right)\)

a. Xét ΔABC vuông tại A, có:
AB2 + AC2 = BC2 (Định lý Py-ta-go)
⇒ 62 + 82 = BC2 (thay số)
⇒ BC2 = 100
⇒ BC = 10
b) Có: AH vuông góc với BC (gt)
⇒ góc AHB = góc AHD (tính chất ....)
Xét ΔAHB và ΔAHD, có:
BH = HD (gt)
góc AHB = AHD (cmt)
AH chung
⇒ ΔAHB = ΔAHD (c.g.c)
⇒ AB = AD (cặp cạnh tương ứng) (đpcm)
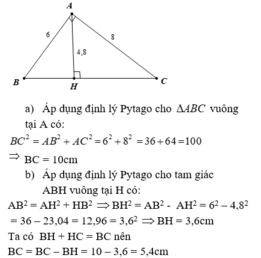
A B C H 6 8 4,8
a) Xét \(\Delta ABC\) vuông tại A
=> BC2 = AB2 + AC2 ( định lý Py - ta - go )
=> BC2 = 62 + 82
=> BC2 = 36 + 64
=> BC2 = 100
=> \(\left\{{}\begin{matrix}BC=10\\BC=-10\end{matrix}\right.\). Vì BC > 0 => BC = 10 cm
Vậy BC = 10 cm
b) Xét \(\Delta AHC\) vuông tại H
=> AC2 = AH2 + HC2 ( định lý Py - ta - go )
=> 82 = 4,82 + HC2
=> 64 = 23,04 + HC2
=> HC2 = 64 - 23,04
=> HC2 = 40,96
=> \(\left\{{}\begin{matrix}HC=6,4\\HC=-6,4\end{matrix}\right.\) . Vì HC > 0 => HC = 6,4 cm
Diện tích \(\Delta AHC\) là : \(\dfrac{1}{2}\) . 4,8 . 6,4 = 15,36 ( cm2 )
Vậy diện tích \(\Delta AHC\) là 15,36 cm2