Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng k 1...

PT

Pham Trong Bach

29 tháng 12 2018

Cho Δ A'B'C' ∼ Δ A''B''C'' theo tỉ số đồng dạng $k_{1}$ , Δ A''B''C'' ∼ Δ ABC theo tỉ số đồng dạng là $k_{2}$ . Hỏi Δ A''B''C'' ∼ Δ A'B'C' và Δ A'B'C' ∼ Δ ABC đồng dạng theo tỉ số nào?

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

29 tháng 12 2018

Đúng(0)

PT

Pham Trong Bach

29 tháng 9 2019

Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Tính tỉ số chu vi của hai tam giác đã cho.

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

29 tháng 9 2019

Ta có: Δ A'B'C' ∼ Δ ABC

Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Đúng(0)

PT

Pham Trong Bach

3 tháng 1 2020

Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Tính tỉ số chu vi của hai tam giác đã cho.

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

3 tháng 1 2020

Ta có:

Δ A'B'C' ∼ Δ ABC Bài tập tổng hợp chương 3 Hình học 8 | Lý thuyết và Bài tập Toán 8 có đáp án

Bài tập tổng hợp chương 3 Hình học 8 | Lý thuyết và Bài tập Toán 8 có đáp án

Đúng(0)

J

JK

8 tháng 9 - olm

cho Δ ABC đồng dạng Δ MNP, AD là tia phân giác góc A, ME là tia phân giác góc M

a) Biết ΔABC đồng dạng ΔMNP theo tỉ lệ số đồng dạng k, chứng minh rằng tỉ số AD : ME cũng bằng k

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

11 giờ trước (8:59)

ΔABC~ΔMNP

=>$\hat{B}=\hat{N};\hat{BAC}=\hat{NMP}$

ta có: $\hat{BAD}=\frac12\cdot\hat{BAC}$ (AD là phân giác của góc BAC)

$\hat{NME}=\frac12\cdot\hat{NMP}$ (ME là phân giác của góc NMP)
mà $\hat{BAC}=\hat{NMP}$

nên $\hat{BAD}=\hat{NME}$

Xét ΔBAD và ΔNME có

$\hat{BAD}=\hat{NME}$

$\hat{B}=\hat{N}$

Do đó: ΔBAD~ΔNME

=>$\frac{AD}{ME}=\frac{BA}{MN}=k$

Đúng(0)

PT

Pham Trong Bach

1 tháng 1 2020

Cho Δ ABC ∼ Δ A'B'C' như hình vẽ. Tính tỉ số đồng dạng ?

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

1 tháng 1 2020

Ta có Δ ABC ∼ Δ A'B'C'. Khi đó tỉ số đồng dạng là

A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.

Đúng(0)

PT

Pham Trong Bach

26 tháng 10 2018

Cho Δ ABC ∼ Δ A'B'C' có tỉ số đồng dạng là k = 5/9 . P và P' lần lượt là chu vi của tam giác ABC và tam giác A'B'C', biết P + P' = 28. Tính P và P'.

A. P = 16cm, P' = 12cm

B. P = 12cm, P' = 16cm

C. P = 10cm, P' = 18cm

D. P = 14cm, P' = 14cm

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

26 tháng 10 2018

Ta có tỉ số chu vi bằng tỉ số đồng dạng nên tam có: P/P' = k = 5/9 ⇒ 9P - 5P' = 0

Mà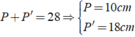 Bài tập tổng hợp chương 3 Hình học 8 | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án C.

Đúng(0)

PT

Pham Trong Bach

9 tháng 1 2017

Cho Δ ABC đồng dạng Δ A'B'C' có AB/A'B' = 2/5. Biết hiệu số chu vi của Δ A'B'C' và Δ ABC là 30cm. Phát biểu nào sau đây đúng? A. Chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm. B. Chu vi của Δ ABC là 50cm, chu vi của Δ A'B'C' là 20cm. C. Chu vi của Δ ABC là 45cm, chu vi của Δ A'B'C' là 75cm. D. Cả 3 đáp án đều sai. ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

9 tháng 1 2017

Ta có: Δ ABC đồng dạng Δ A'B'C'

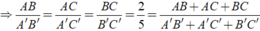
Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Khi đó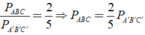 Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Mà PA'B'C' - PABC = 30cm.

Suy ra

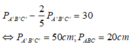
Bài tập: Khái niệm hai tam giác đồng dạng | Lý thuyết và Bài tập Toán 8 có đáp án

Vậy chu vi của Δ ABC là 20cm, chu vi của Δ A'B'C' là 50cm.

Chọn đáp án A.

Đúng(0)

PT

Pham Trong Bach

27 tháng 7 2019

Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Cho biết hiệu chu vi của hai tam giác trên là 40dm. Tính chu vi của hai tam giác đã cho

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

27 tháng 7 2019

Đúng(0)

PT

Pham Trong Bach

13 tháng 11 2017

Cho tam giác Δ A'B'C' ∼ Δ ABC theo tỉ số đồng dạng là k = 3/5. Cho biết hiệu chu vi của hai tam giác trên là 40dm. Tính chu vi của hai tam giác đã cho

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

13 tháng 11 2017

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP