Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sủa lại là: Chứng minh 4 điểm D,E,F,K cùng nằm trên một đường tròn

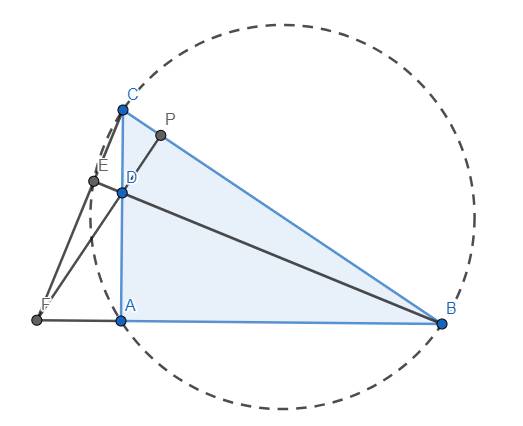
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.

A B C K E D M F G
Gọi đường tròn đó cắt cạnh AB tại G khác B. Vì \(\Delta\)ABC cân tại A nên GD // BC.
Dựng hình bình hành AEFD. Khi đó DF // AE // BC. Suy ra F,D,G thẳng hàng, từ đây ^KDF = ^KBG (1)
Ta có ^DBK = ^DCK = ^ECA và ^DKB = ^DCB = ^EAC, suy ra \(\Delta\)BKD ~ \(\Delta\)CAE (g.g)
Suy ra \(\frac{KD}{DF}=\frac{KD}{AE}=\frac{KB}{AC}=\frac{KB}{BA}\), kết hợp với (1) ta được \(\Delta\)DKF ~ \(\Delta\)BKA (c.g.c)
Từ đó \(\Delta\)KFA ~ \(\Delta\)KDB (c.g.c). Do vậy ^KAF = ^KBD = ^KCD = ^KEF
Suy ra ^AKE = ^AFE = ^DAF = ^MAD (Vì A,M,F thẳng hàng) (đpcm).

AK giao BC tại F'
->ABF' = ABH + HAF' = ACB + CAF' = 180 - AF'C = AF'B nên AB = BF'. Mà AB = BF =>F trùng F'
Vậy A, K, F thẳng hàng

A B C D E F G
Gọi AE cắt CD tại G. Dễ thấy \(\frac{AE}{AG}=\frac{BE}{BC}=\frac{3}{4},FG=DC\), do đó:
\(\frac{1}{2}AE.AF.\sin\widehat{EAF}=S_{AEF}=\frac{3}{4}S_{AFG}=\frac{3}{4}S_{ADC}=\frac{3}{8}AB.BC\)
Suy ra \(\sin\widehat{EAF}=\frac{3}{4}.\frac{AB.BC}{AE.AF}=\frac{3}{4}.\frac{xy}{\sqrt{x^2+\frac{9}{16}y^2}.\sqrt{y^2+\frac{1}{9}x^2}}\) \(\left(x=AB,y=BC\right)\)
\(\le\frac{3}{4}.\frac{xy}{xy+\frac{1}{4}xy}=\frac{3}{5}\) (BĐT Bunhiacopxki)
Vì \(0^0< \widehat{EAF}< 90^0\) nên \(max\widehat{EAF}=arc\sin\left(\frac{3}{5}\right)\approx36,87^0\)
Dấu "=" xảy ra khi và chỉ khi \(\frac{x}{y}=\frac{\frac{3}{4}y}{\frac{1}{3}x}\Leftrightarrow\frac{x}{y}=\frac{3}{2}\)hay \(\frac{AB}{BC}=\frac{3}{2}\Rightarrow\frac{AB}{AC}=\frac{3\sqrt{13}}{13}\)

Đặt \(\left\{{}\begin{matrix}S_{BDF}=x\\S_{CEF}=y\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}S_{ADF}=3x\\S_{AEF}=4y\\S_{ABF}=4x\\S_{ACF}=5y\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}S_{ABE}=4x+4y=\dfrac{4}{5}S_{ABC}\\S_{ACD}=3x+5y=\dfrac{3}{4}S_{ABC}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}20x+20y=4S_{ABC}\\12x+20y=3S_{ABC}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=8x=2S_{ABF}\)
Xong