HG
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2019
Do \(0< a< \frac{\pi}{2}\Rightarrow sina>0\)
\(sin^2a+cos^2a=1\Rightarrow sina=\sqrt{1-cos^2a}=\sqrt{1-\left(\frac{15}{17}\right)^2}=\frac{8}{17}\)
\(cos2a=2cos^2a-1=2.\left(\frac{15}{17}\right)^2-1=\frac{161}{289}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2020
\(\frac{3\pi}{4}< a< \pi\Rightarrow\left\{{}\begin{matrix}sina>0\\cosa< 0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}sin^2a+cos^2a=1\\2sina.cosa=-\frac{4}{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}sin^2a+cos^2a=1\\cosa=-\frac{2}{5sina}\end{matrix}\right.\)
\(\Rightarrow sin^2a+\frac{4}{25sin^2a}=1\)
\(\Leftrightarrow25sin^4a-25sin^2a+4=0\) \(\Rightarrow\left[{}\begin{matrix}sin^2a=\frac{4}{5}\\sin^2a=\frac{1}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}sina=\frac{2}{\sqrt{5}}\\cosa=-\frac{1}{\sqrt{5}}\end{matrix}\right.\\\left\{{}\begin{matrix}sina=\frac{1}{\sqrt{5}}\\cosa=-\frac{2}{\sqrt{5}}\end{matrix}\right.\end{matrix}\right.\)
Mà \(\frac{3\pi}{4}< a< \pi\Rightarrow\pi< a+\frac{\pi}{4}< \frac{5\pi}{4}\Rightarrow sina+cosa< 0\)
\(\Rightarrow\left\{{}\begin{matrix}sina=\frac{1}{\sqrt{5}}\\cosa=-\frac{2}{\sqrt{5}}\end{matrix}\right.\)
TN
24 tháng 7 2023
tại sao phải cộng thêm pi/4, mà tại sao cộng thêm pi/4 thì lại suy ra đc sina+cosa<0 vậy ạ
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2020
\(0< a< \frac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\frac{4}{5}\)
\(\Rightarrow tana=\frac{sina}{cosa}=\frac{3}{4}\) ; \(cota=\frac{1}{tana}=\frac{4}{3}\)
\(\Rightarrow A=\frac{\frac{4}{3}+\frac{3}{4}}{\frac{4}{3}-\frac{3}{4}}=...\)
\(\frac{2sina+3cosa}{4sina-5cosa}=\frac{\frac{2sina}{cosa}+\frac{3cosa}{cosa}}{\frac{4sina}{cosa}-\frac{5cosa}{cosa}}=\frac{2tana+3}{4tana-5}=\frac{2.3+3}{4.3-5}=...\)
\(A=\frac{2sin^2a-3cos^2a}{sin^2a-2sina.cosa-cos^2a}=\frac{\frac{2sin^2a}{sin^2a}-\frac{3cos^2a}{sin^2a}}{\frac{sin^2a}{sin^2a}-\frac{2sina.cosa}{sin^2a}-\frac{cos^2a}{sin^2a}}=\frac{2-3cot^2a}{1-2cota-cot^2a}=\frac{2-3.3^2}{1-2.3-3^2}=...\)
TH
Trần Hoàng Trung
VIP
19 tháng 8
Khi \(cot \left(\right. a \left.\right) = 3\) và \(0^{\circ} < a < 90^{\circ}\), ta có thể áp dụng một số tính chất lượng giác để tính các giá trị khác liên quan đến góc \(a\).
1. Định nghĩa \(cot \left(\right. a \left.\right)\)
Ta biết rằng:
\(cot \left(\right. a \left.\right) = \frac{1}{tan \left(\right. a \left.\right)}\)
Do đó, từ \(cot \left(\right. a \left.\right) = 3\), ta có:
\(tan \left(\right. a \left.\right) = \frac{1}{3}\)
2. Tính giá trị các hàm lượng giác khác
Dựa trên giá trị \(tan \left(\right. a \left.\right) = \frac{1}{3}\), ta có thể tính giá trị của các hàm lượng giác khác như \(sin \left(\right. a \left.\right)\), \(cos \left(\right. a \left.\right)\), và \(sec \left(\right. a \left.\right)\).
a. Tính \(sin \left(\right. a \left.\right)\) và \(cos \left(\right. a \left.\right)\)
Ta sử dụng định lý Pythagoras trong tam giác vuông với cạnh đối và cạnh kề:
\(tan \left(\right. a \left.\right) = \frac{\text{c}ạ\text{nh}\&\text{nbsp};đ \overset{ˊ}{\hat{\text{o}}} \text{i}}{\text{c}ạ\text{nh}\&\text{nbsp};\text{k} \overset{ˋ}{\hat{\text{e}}}} = \frac{1}{3}\)
Giả sử cạnh đối là 1 và cạnh kề là 3, ta có thể tính cạnh huyền \(h\) theo định lý Pythagoras:
\(h = \sqrt{1^{2} + 3^{2}} = \sqrt{1 + 9} = \sqrt{10}\)
Vậy:
\(sin \left(\right. a \left.\right) = \frac{\text{c}ạ\text{nh}\&\text{nbsp};đ \overset{ˊ}{\hat{\text{o}}} \text{i}}{h} = \frac{1}{\sqrt{10}}\)\(cos \left(\right. a \left.\right) = \frac{\text{c}ạ\text{nh}\&\text{nbsp};\text{k} \overset{ˋ}{\hat{\text{e}}}}{h} = \frac{3}{\sqrt{10}}\)
b. Tính \(sec \left(\right. a \left.\right)\) và \(csc \left(\right. a \left.\right)\)
- \(sec \left(\right. a \left.\right) = \frac{1}{cos \left(\right. a \left.\right)} = \frac{\sqrt{10}}{3}\)
- \(csc \left(\right. a \left.\right) = \frac{1}{sin \left(\right. a \left.\right)} = \sqrt{10}\)
3. Tóm tắt kết quả
- \(tan \left(\right. a \left.\right) = \frac{1}{3}\)
- \(sin \left(\right. a \left.\right) = \frac{1}{\sqrt{10}}\)
- \(cos \left(\right. a \left.\right) = \frac{3}{\sqrt{10}}\)
- \(sec \left(\right. a \left.\right) = \frac{\sqrt{10}}{3}\)
- \(csc \left(\right. a \left.\right) = \sqrt{10}\)
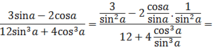
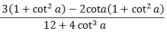
Do \(0< a< \frac{\pi}{2}\Rightarrow sina>0\)
\(cot^2a+1=\frac{1}{sin^2a}\Rightarrow sin^2a=\frac{1}{1+cot^2a}\)
\(\Rightarrow sina=\frac{1}{\sqrt{1+cot^2a}}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}\)