VN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
17 tháng 8 2019
- Hầu như các OLmers toàn tầm khoảng 2k4 đến 2k9 nên mk nghĩ là câu này của bn khó cs ai TL đc =))
- Mk nghĩ bn nên vào web : H để đăng bài ! Vì mk thấy ở đó chuyên giải mấy bài khó -,-
- Hoăc bn cs thể nhờ https://olm.vn/thanhvien/linhchi_nguyenthi1997 ( cj này là quản lý của olm và hay giải mấy bài khó )
Ckuc bn hok tốt =))
T
1
AH
Akai Haruma
Giáo viên
31 tháng 1 2017
Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
LM
0
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2019
\(I=\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{6}}\frac{sin^2x.cosx+2sin2x}{\left(f\left(sinx\right)\right)^2}dx=\int\limits^{\frac{\pi}{3}}_{\frac{\pi}{6}}\frac{\left(sin^2x+4sinx\right).cosx}{\left(f\left(sinx\right)\right)^2}dx\)
Đặt \(sinx=t\Rightarrow cosx.dx=dt;\left\{{}\begin{matrix}x=\frac{\pi}{6}\Rightarrow t=\frac{1}{2}\\x=\frac{\pi}{3}\Rightarrow t=\frac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}\frac{\left(t^2+4t\right)}{f^2\left(t\right)}dt=\int\limits^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}\frac{\left(x^2+4x\right)}{f^2\left(x\right)}dx\)
Lại có:
\(x+x.f'\left(x\right)=2f\left(x\right)-4\Leftrightarrow x+4=2f\left(x\right)-x.f'\left(x\right)\)
\(\Leftrightarrow x^2+4x=2x.f\left(x\right)-x^2.f'\left(x\right)\)
\(\Leftrightarrow\frac{x^2+4x}{f^2\left(x\right)}=\frac{2x.f\left(x\right)-x^2.f'\left(x\right)}{f^2\left(x\right)}=\left(\frac{x^2}{f\left(x\right)}\right)'\)
\(\Rightarrow I=\int\limits^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}\left(\frac{x^2}{f\left(x\right)}\right)'dx=\frac{x^2}{f\left(x\right)}|^{\frac{\sqrt{3}}{2}}_{\frac{1}{2}}=\frac{\left(\frac{\sqrt{3}}{2}\right)^2}{f\left(\frac{\sqrt{3}}{2}\right)}-\frac{\left(\frac{1}{2}\right)^2}{f\left(\frac{1}{2}\right)}=\frac{3}{4b}-\frac{1}{4a}\)
AH
Akai Haruma
Giáo viên
20 tháng 11 2017
Bạn viết đề bài rõ ràng hộ mình nhé đọc đề không dịch được.
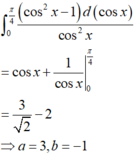
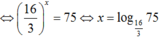
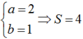
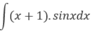
mọi người giúp e với ạ