Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có hình vẽ
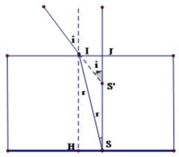
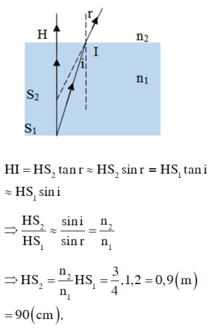
Từ hình vẽ ta thấy rằng IJ = JS’.tani; IJ = JS.tanr
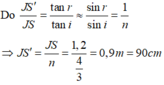

Chọn đáp án B.
Ánh sáng mặt trời chiếu qua mặt nước đập vào viên sỏi, phản xạ, lên rồi khúc xạ ra ngoài không khí. Nếu để mắt hứng các tia khúc xạ thì nhìn thấy ảnh ảo của viên sỏi ở dưới mặt nước (mặt nước đóng vai trò lưỡng chất phẳng nước-không khí). Vì mắt đồng thời nhận được hai chùm sáng phản xạ và khúc xạ trùng nhau nên có cảm giác như viên sỏi được nâng lên gần với mặt nước.
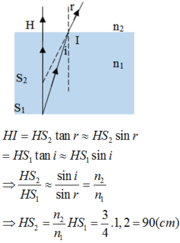

Đáp án A
Ánh sáng mặt trời chiếu qua mặt nước đập vào viên sỏi, phản xạ, lên rồi khúc xạ ra ngoài không khí. Nếu để mắt hứng các tia khúc xạ thì nhìn thấy ảnh ảo của viên sỏi ở dưới mặt nước (mặt nước đóng vai trò lưỡng chất phẳng nước-không khí). Vì mắt đồng thời nhận được hai chùm sáng phản xạ và khúc xạ trùng nhau nên có cảm giác như viên sỏi được nâng lên gần với mặt nước.

H S I i i gh 20cm
Để mắt người quan sát ở mặt nước không thấy vật sáng ở đáy chậu thì không có tia sáng nào từ vật S thoát ra ngoài, như vậy ít nhất tia tới SI cho tia khúc xạ là là mặt nước như hình vẽ, khi đó góc \(i=i_{gh}\)
=> \(\sin i = \sin i_{gh}=\frac{1}{n}=\frac{3}{4}\)
=>\(\tan i = \frac{3}{\sqrt 7}\)
Mà \(\tan i = \frac{HI}{HS}\Rightarrow HS = HI/\tan i = 20/\frac{3}{\sqrt 7}=\frac{20\sqrt 7}{3}\)cm.
Vậy chiều sâu của nước trong chậu là HS = \(\frac{20\sqrt 7}{3}\)cm.

Chọn C
Xét chùm tia tới tới mặt nước gần như vuông góc với mặt nước khi đó góc tới i nhỏ dẫn đến sini gần bằng tani
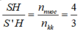
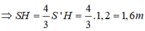

Quan sát và phân tích hiện tượng nước chảy ở ống nhỏ giọt ta thấy: đầu tiên giọt nước to dần nhưng chưa rơi xuống, đó là vì có các lực căng bề mặt tác dụng lên đường biên \(BB'\) của giọt nước, các lực này có xu hướng kéo co mặt ngoài của giọt nước lại, vì thế hợp lực của chúng hướng lên trên và có độ lớn \(\text{F=σl}\), với \(\text{l=πd}\),( \(d\) là đường kính miệng).
Đúng lúc giọt nước tách ra và rơi xuống thì trọng lượng \(P\) của giọt nước bằng lực căng bề mặt \(F\);
\(F=P\),
suy ra :
\(\text{σπd=mg}\) hay \(\sigma=\frac{mg}{\pi d}\left(1\right)\)
với \(m\) là khối lượng của \(1\) giọt nước. Theo đề bài \(2cm^3\) chứa \(200\) giọt nước, khối lượng \(2cm^3\) bằng \(2g\); vì vậy khối lượng của một giọt nước bằng
\(m=\frac{2g}{200}=0,01g=10^{-5}kg\)
Thay số vào (1) ta được: \(\sigma=\frac{9,8.10^{-5}}{3,14.0,4.10^{-3}}\approx0,078N\text{/}m\)
Hệ số căng bề mặt của nước bằng \(0,078N\text{/}m\)