
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
a) Đúng vì vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ.
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).

c) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì a // c và b // c do đó a // b tức là \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương , cùng chiều đo đó cùng hướng.

a) Gọi theo thứ tự ∆1, ∆2, ∆3 là giá của các vectơ ,
,
cùng phương với
=> ∆1 //∆3 ( hoặc ∆1 = ∆3 ) (1)
cùng phương với
=> ∆2 // ∆3 ( hoặc ∆2 = ∆3 ) (2)
Từ (1), (2) suy ra ∆1 // ∆2 ( hoặc ∆1 = ∆2 ), theo định nghĩa hai vectơ ,
cùng phương.
Vậy câu a) đúng.
b) Câu này cũng đúng.

Đáp án B
Hai vecto a → ; b → ngược hướng
⇔ a → ; b → = 180 0
Ta a → . b → = a → . b → . c os a → ; b → = a → . b → . c os 180 0 = − a → . b →

Ta có: a → , b → ≠ 0 → ⇒ a → . b → ≠ 0
Do đó: a → . b → = a → . b → . cos a → , b →
Để a → . b → = a → . b → ⇔ cos a → , b → = 1 ⇔ a → , b → = 0 °
Khi đó a → , b → cùng hướng
Chọn A

Ta có: ( a → . b → ) . c → là một vecto cùng phương với vecto c → .
a → . ( b → . c → ) là một vecto cùng phương với vecto a → .
Vì hai vecto a → ; c → không cùng phương nên 2 vecto ( a → . b → ) . c → và a → . ( b → . c → ) không cùng phương nên không thể bằng nhau.
Chọn B.
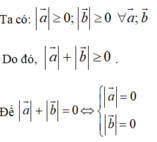

Ta có: a → ⊥ b → ⇔ ( a → ; b → ) = 90 0 ⇔ a → . b → = a → . b → . c os ( a → ; b → ) = 0
Chọn B.