Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta chứng minh BĐT
( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9
Áp dụng BĐT Cô – si cho hai số dương ta có:
a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng
= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3
Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có 1 + b 2 ≥ 2 b
Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )
Tương tự ta có:
b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )
Cộng từng vế của (1), (2) và (3) ta có:
a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3

Dễ vậy mà ko làm đc àk
\(a_1.a_2=b_1.b_2\Rightarrow\frac{a_1}{b_1}=\frac{b_2}{a_2}\)
\(\Rightarrow\frac{a_1}{b_1}+\frac{a_2}{b_2}=\frac{b_2}{a_2}+\frac{a_2}{b_2}\ge2\sqrt{\frac{b_2}{a_2}.\frac{a_2}{b_2}}=2\) (AM - GM)
có a1.a2=b1.b2
=> a1/b1=b2/a2
có \(\frac{a1}{b1}+\frac{a2}{b2}=\frac{b2}{a2}+\frac{a2}{b2}\)
áp dụng bất đẳng thức cosi cho 2 số dương có
\(\frac{b2}{a2}+\frac{a2}{b2}\ge2\sqrt{\frac{b2}{a2}.\left(\frac{a2}{b2}\right)}=2\)(đpcm)

3, \(\sqrt{\frac{a}{b+c}}=\sqrt{\frac{a^2}{a\left(b+c\right)}}\Rightarrow\frac{1}{\sqrt{\frac{a}{b+c}}}=\sqrt{\frac{a\left(b+c\right)}{a^2}}.\)
Áp dụng bất đẳng thức Cô si ta có : \(\sqrt{\frac{a\left(b+c\right)}{a^2}}\le\frac{a+b+c}{2a}\Rightarrow\sqrt{\frac{a}{b+c}}\ge\frac{2a}{a+b+c}\left(1\right).\)
Chứng minh tương tự ta có : \(\sqrt{\frac{b}{a+c}}\ge\frac{2b}{a+b+c}\left(2\right).\); \(\sqrt{\frac{c}{a+b}}\ge\frac{2c}{a+b+c}\left(3\right).\)
Cộng vế với vế các bất đẳng thức cùng chiều ta được:
\(\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{a+c}}+\sqrt{\frac{c}{a+b}}\ge\frac{2\left(a+b+c\right)}{a+b+c}=2.\)( đpcm )
dấu " = " xẩy ra khi a = b = c > 0

Câu 2:
\( P = \dfrac{{a - b}}{{\sqrt a + \sqrt b }} + \dfrac{{a\sqrt a - b\sqrt b }}{{a + b + \sqrt {ab} }}\\ P = \dfrac{{\left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)}}{{\left( {\sqrt a + \sqrt b } \right)}} + \dfrac{{\left( {\sqrt a - \sqrt b } \right)\left( {a + \sqrt {ab} + b} \right)}}{{a + b + \sqrt {ab} }}\\ P= \sqrt a - \sqrt b + \sqrt a - \sqrt b \\ P = 2\sqrt a - 2\sqrt b \)
Câu 1:
\(a)\left( {3\sqrt {\dfrac{3}{5}} - \sqrt {\dfrac{5}{3}} + \sqrt 5 } \right)2\sqrt 5 + \dfrac{2}{3}\sqrt {75} \\
= 6\sqrt {\dfrac{{15}}{5}} - 2\sqrt {\dfrac{{25}}{3}} + 10 + \dfrac{{10\sqrt 3 }}{3}\\
= 6\sqrt 3 - \dfrac{{10}}{{\sqrt 3 }} + 10 + \dfrac{{10\sqrt 3 }}{3}\\
= 6\sqrt 3 - \dfrac{{10\sqrt 3 }}{3} + 10 + \dfrac{{10\sqrt 3 }}{3}\\
= 6\sqrt 3 + 10\\
b){\left( {\sqrt 3 - 1} \right)^2} - \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} + \sqrt {{{\left( { - 3} \right)}^2}.3} \\
= 3 - 2\sqrt 3 + 1 - \sqrt 3 + 1 + \sqrt {{3^3}} \\
= 5 - 3\sqrt 3 + 3\sqrt 3 \\
= 5\)

\(a,\left(3\sqrt{\frac{3}{5}}-\sqrt{\frac{5}{3}}+\sqrt{5}\right)2\sqrt{5}+\frac{2}{3}\sqrt{75}\)
\(=6\sqrt{3}-\frac{10\sqrt{3}}{3}+10+\frac{10\sqrt{3}}{3}\)
\(=6\sqrt{3}+10\)
\(b,\left(\sqrt{3}-1\right)^2-\sqrt{\left(1-\sqrt{3}\right)^2}+\sqrt{\left(-3\right)^2.3}\)
\(=\left(\sqrt{3}^2-2.\sqrt{3}.1+1^2\right)-|1-\sqrt{3}|+\sqrt{27}\)
\(=4-2\sqrt{3}-\sqrt{3}+1+3\sqrt{3}\)
\(=5\)
\(P=\frac{a-b}{\sqrt{a}+\sqrt{b}}+\frac{a\sqrt{a}-b\sqrt{b}}{a+b+\sqrt{ab}}\left(a\ge0;b\ge0;a\ne b\right)\)
\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}+\frac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{a+b+\sqrt{ab}}\)
\(=\sqrt{a}-\sqrt{b}+\sqrt{a}-\sqrt{b}\)
\(=2\sqrt{a}-2\sqrt{b}\)
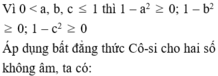
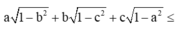
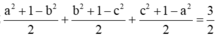

a1/a2 = b1/b2 = c1/c2 = k
a1=k.a2, b1=k.b2, c1=k.c2
Biểu thức trở thành
√(k.a2 + k.b2 + k.c2).(a2 + b2 + c2)= √k.a2.a2 + √k.b2.b2 + √k.c2.c2
√k.(a2+b2+c2)2 = a2. √k + b2. √k + c2. √k
(a2+b2+c2). √k = (a2+b2+c2). √k (hiển nhiên đúng)
Suy ra điều phải chứng minh