Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
Ta có
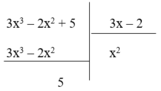
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
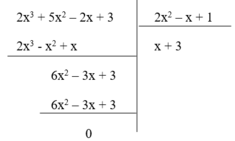
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D

2x^3+3x^2-x+a x^2+x-1 2x+1 2x^3+x^2 - - 2x^2-x+a 2x^2+x -2x+a -2x-1 - a+1
Để \(A\left(x\right)⋮B\left(x\right)\Leftrightarrow a+1=0\)
\(\Leftrightarrow a=-1\)
Vậy ...
2x^3+3x^2-x+a x^2+x-1 2x+1 2x^3+x^2 - - 2x^2-x+a 2x^2+x -2x+a -2x-1 - a+12x^3+3x^2-x+a x^2+x-1 2x+1 2x^3+x^2 - - 2x^2-x+a 2x^2+x -2x+a -2x-1 - a+1
Để \(A \left(\right. x \left.\right) B \left(\right. x \left.\right) \Leftrightarrow a + 1 = 0\)
\(\Leftrightarrow a = - 1\)

a) \(x^3+x^2-x+a=\left(x^2-x+1\right)\left(x+2\right)+\left(a-2\right)\).
Đa thức trên chia hết cho \(x+2\) khi và chỉ khi a = 2.
b) \(x^3+ax^2+2x+b=\left(x^2+x+1\right)\left(x+1\right)+\left(a-2\right)x^2+\left(b-1\right)\) chia hết cho \(x^2+x+1\) khi và chỉ khi:
\(\frac{a-2}{1}=\frac{0}{1}=\frac{b-1}{1}\Leftrightarrow a=2;b=1\).
c) Tương tự.

a) ta có (2n2-n+2)/(2n+1)=n-1(dư 3)
vậy muốn 2n2-n+2 chia hết cho 2n+1 thì 2n+1ϵƯ(3)
mà Ư(3)={-3;-1;1;3}
nên
2n+1=-3 và 2n+1=-1 và 2n+1=1 và 2n+1=3
=> 2n=-4 và 2n=-2 và 2n=0 và 2n=2
=> n=-2 và n=-1 và n=0 và n=1
vậy nϵ{-2;-1;0;1}
b) ta có x3+x2-x+a/(x+1)2=x-1(dư -x2-2x+a)
mà \(x^2-2x+a-\left(-x^2-2x-1\right)=a+1\)
và muốn \(x^3+x^2-x+a\) chia hết cho \(\left(x+1\right)^2\)thì a+1=0
=> a=-1

a: \(\Leftrightarrow3x^3+x^2+9x^2+3x-3x-1+a-4⋮3x+1\)
=>a-4=0
hay a=4
c: \(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{3;1;5;-1\right\}\)

Ta có
Vì phần dư R = 0 nên Phép chia đa thức (2 x 3 – 26x – 24) cho đa thức x 2 + 4x + 3 là phép chia hết.
Do đó (I) đúng.
Lại có
Nhận thấy phần dư R = 0 nên phép chia đa thức ( x 3 – 7x + 6) cho đa thức x + 3 là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: A