Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
P(x) = 2x4 –x - 2x3 + 1
Q(x) = 5x2 – x3 + 4x
H(x) = -2x4 + x2 + 5.
Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:
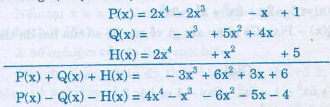
ta có:
P(x) = 2x4 –x – 2x3 + 1
Q(x) = 5x2 – x3 + 4x
H(x) = -2x4 + x2 + 5.
Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:


f(x) +g(x) + h(x)
=(2x4 - x3 + x - 3 + 5x5) + (-x5 + 5x2 +4x + 2 + 3x5) + (x2 + x + 1 + 2x3 + 3x4)
= 2x4 - x3 + x - 3 + 5x5 +(-x5) + 5x2 +4x + 2 + 3x5 + x2 + x + 1 + 2x3 + 3x4
= 7x5 + 5x4 + x3 +x2 + 6x
f(x) - g(x) - h(x)
=(2x4 - x3 + x - 3 + 5x5) - (-x5 + 5x2 +4x + 2 + 3x5) - (x2 + x + 1 + 2x3 + 3x4)
=2x4 - x3 + x - 3 + 5x5 +x5 - 5x2 -4x - 2 -3x5 - x2 - x - 1 - 2x3 - 3x4
= 3x5 - x4 - 3x3 - 6x2 - 4x - 6

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !

1.a. \(3^2-2x-5=0\Rightarrow-2x=0-9+5=-4\)
\(\Rightarrow-x=-\dfrac{4}{2}=-2\Rightarrow x=2\)
Vậy x nghiệm của đa thức \(3^2-2x-5\) là 2
b. \(x^2-5x+4=0\Rightarrow x=\dfrac{-\left(-5\right)\pm\sqrt{\left(-5\right)^2-4\cdot1\cdot4}}{2\cdot1}=\dfrac{5\pm\sqrt{25-16}}{2}=\dfrac{5\pm\sqrt{9}}{2}=\dfrac{5\pm3}{2}=\left[{}\begin{matrix}\dfrac{5+3}{2}=\dfrac{8}{2}=4\\\dfrac{5-3}{2}=\dfrac{2}{2}=1\end{matrix}\right.\)
Vậy nghiệm của đa thức \(x^2-5x+4\) là 1 hoặc 4
c. \(x^2+4x+7=0\Rightarrow x=\dfrac{-4\pm\sqrt{4^2-4\cdot1\cdot7}}{2\cdot1}=\dfrac{-4\pm\sqrt{16-28}}{2}=\dfrac{-4\pm\sqrt{-12}}{2}\Rightarrow x\notin Z\)
Vậy \(x\notin Z\)
2.a. \(P\left(x\right)=3\cdot x^4-x^3+4x^2+2x+1=3x^4-x^3+4x^2+2x+1\)
\(P\left(x\right)+Q\left(x\right)=\left(3x^4-x^3+4x^2+2x+1\right)+\left(-2x^4-x^2+x-2\right)\)
\(=3x^4-x^3+4x^2+2x+1-2x^4-x^2+x-2\)
\(=x^4-x^3+3x^2+3x-1\)
Vậy \(P\left(x\right)+Q\left(x\right)=x^4-x^3+3x^2+3x-1\)
b. \(Q\left(x\right)-H\left(x\right)=-2x^4-2\)
\(\Rightarrow-H\left(x\right)=-2x^4-2-Q\left(x\right)\)
\(\Rightarrow-H\left(x\right)=-2x^4-2-\left(-2x^4-x^2+x-2\right)\)
\(\Rightarrow-H\left(x\right)=-2x^4-2+2x^4+x^2-x+2\)
\(\Rightarrow-H\left(x\right)=x^2-x\Rightarrow H\left(x\right)=-x^2+x\)
Vậy \(H\left(x\right)=x^2+x\)
c. \(H\left(x\right)=0\Rightarrow x^2+x=0\Rightarrow x\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy nghiệm của đa thức H(x) là 0 hoặc -1

Bài 1:
Thay x=1 vào đa thức F(x) ta được:
F(1) = 14+2.13-2.12-6.1+5 = 0
=> x=1 là nghiệm của đa thức F(x)
Tương tự ta thế -1; 2; -2 vào đa thức F(x)
Vậy x=1 là nghiệm của đa thức F(x)
Sắp xếp các đa thức theo lũy thừa giảm dần rồi xếp các số hạng đồng dạng theo cùng cột dọc ta được:
P(x) = 2x4– 2x3 – x +1
Q(x) = – x3 + 5x2+ 4x
H(x) = –2x4 + x2+ 5
Đặt và thực hiện các phép tính ta có:
Vậy: P(x) + Q(x) + H(x) = -3x3+ 6x2 + 3x + 6.
P(x) - Q(x) - H(x) = 4x4 - x3 - 6x2 – 5x – 4.