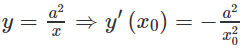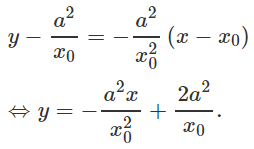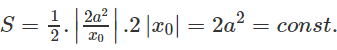Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=\frac{-1}{\left(x-1\right)^2}\)
a/ Gỉa sử tại \(A\left(a;\frac{2a-1}{a-1}\right)\) đồ thị hàm số có tiếp tuyến thỏa mãn yêu cầu
Phương trình d tiếp tuyến:
\(y=\frac{-1}{\left(a-1\right)^2}\left(x-a\right)+\frac{2a-1}{a-1}\)
Giao điểm của d với \(x=1\) và \(y=2\) lần lượt có tọa độ \(B\left(1;\frac{2a}{a-1}\right)\) và \(C\left(2a-1;2\right)\)
\(IB=\sqrt{\left(1-1\right)^2+\left(\frac{2a}{a-1}-2\right)^2}=\frac{2}{\left|a-1\right|}\)
\(IC=\sqrt{\left(2a-1-1\right)^2+\left(2-2\right)^2}=2\left|a-1\right|\)
\(BC=\sqrt{IB^2+IC^2}=\sqrt{\frac{4}{\left(a-1\right)^2}+4\left(a-1\right)^2}\)
\(\Rightarrow P_{IBC}=IB+IC+BC=\frac{2}{\left|a-1\right|}+2\left|a-1\right|+\sqrt{\frac{4}{\left(a-1\right)^2}+4\left(a-1\right)^2}\)
\(\Rightarrow P_{IBC}\ge2\sqrt{\frac{2}{\left|a-1\right|}.2\left|a-1\right|}+\sqrt{2\sqrt{\frac{4}{\left(a-1\right)^2}.4\left(a-1\right)^2}}=4+2\sqrt{2}\)
Dấu "=" xảy ra khi \(\left(a-1\right)^2=1\Rightarrow a=0\)
Phương trình d: \(y=-x+1\)
b/ Có một cách ứng dụng, đó là tiếp tuyến có khoảng cách đến giao điểm của hai tiệm cận là lớn nhất khi tiếp tuyến đó vuông góc với đường phân giác hai tiệm cận (đường phân giác có cắt đồ thị hàm số)
\(\Rightarrow\) Nếu hàm số đồng biến thì tiếp tuyến này có hệ số góc bằng 1, hàm số nghịch biến thì tiếp tuyến này có hệ số góc bằng -1
Ví dụ trong bài này, hàm số nghịch biến nên ta có ngay tiếp tuyến cần tìm có dạng \(y=-x+b\)
Mặt khác \(y'\left(x_0\right)=-1\Rightarrow\frac{-1}{\left(x_0-1\right)^2}=-1\Rightarrow\left[{}\begin{matrix}x_0=0\\x_0=2\end{matrix}\right.\)
Phương trình tiếp tuyến: \(\left[{}\begin{matrix}y=-x+1\\y=-x+5\end{matrix}\right.\)
// Làm theo kiểu bình thường:
Gọi \(A\left(a;\frac{2a-1}{a-1}\right)\) là điểm mà tại đó tiếp tuyến có tính chất thoả mãn yêu cầu
Phương trình tiếp tuyến d: \(y=\frac{-1}{\left(a-1\right)^2}\left(x-a\right)+\frac{2a-1}{a-1}\)
\(\Leftrightarrow x+\left(a-1\right)^2y-2a^2+2a-1=0\)
Áp dụng công thức khoảng cách:
\(d\left(I;d\right)=\frac{\left|1+2\left(a-1\right)^2-2a^2+2a-1\right|}{\sqrt{1^2+\left(a-1\right)^4}}=\frac{2\left|a-1\right|}{\sqrt{1+\left(a-1\right)^4}}=\frac{2}{\sqrt{\frac{1}{\left(a-1\right)^2}+\left(a-1\right)^2}}\le\frac{2}{\sqrt{2\sqrt{\frac{1}{\left(a-1\right)^2}\left(a-1\right)^2}}}=\sqrt{2}\)
Dấu "=" xảy ra khi \(\left(a-1\right)^4=1\Rightarrow\left[{}\begin{matrix}a=0\\a=2\end{matrix}\right.\)
Phương trình tiếp tuyến: \(\left[{}\begin{matrix}y=-x+1\\y=-x+5\end{matrix}\right.\)
Rõ ràng cách này dài hơn rất nhiều

Gọi \(A_1\) và \(A_2\) lần lượt là điểm đối xứng A qua \(d_1\) và \(d_2\Rightarrow\left\{{}\begin{matrix}A_1\left(4;3\right)\\A_2\left(\frac{7}{5};\frac{24}{5}\right)\end{matrix}\right.\)
Với B bất kì thuộc d1 và C bất kì thuộc d2, ta luôn có \(\left\{{}\begin{matrix}AB=A_1B\\AC=A_2C\end{matrix}\right.\)
\(\Rightarrow T=AB+BC+AC=A_1B+BC+CA_2\ge A_1A_2\)
\(\Rightarrow T_{min}=A_1A_2\) khi \(A_1;B;C;A_2\) thẳng hàng hay B, C lần lượt là giao điểm của đường thẳng \(A_1A_2\) và d1; d2
\(\overrightarrow{A_1A_2}=\left(-\frac{13}{5};\frac{9}{5}\right)\Rightarrow A_1A_2\) có 1 vtpt là \(\left(9;13\right)\)
Phương trình A1A2:
\(9\left(x-4\right)+13\left(y-3\right)=0\Leftrightarrow9x+13y-75=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}y=x\\9x+13y-75=0\end{matrix}\right.\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}y=2x\\9x+13y-75=0\end{matrix}\right.\)

Gọi \(A\left(-1;0\right)\) là 1 điểm thuộc d1
Gọi \(A'\left(a;b\right)\) là ảnh của A qua phép vị tự tâm I tỉ số k
\(\Rightarrow\left\{{}\begin{matrix}a-2=k\left(-1-2\right)\\b-1=k\left(0-1\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3k+2\\b=-k+1\end{matrix}\right.\)
Do A' thuộc d2 nên thay vào pt d2 ta được:
\(-3k+2-2\left(-k+1\right)+4=0\)
\(\Leftrightarrow k=4\)

Tham khảo:
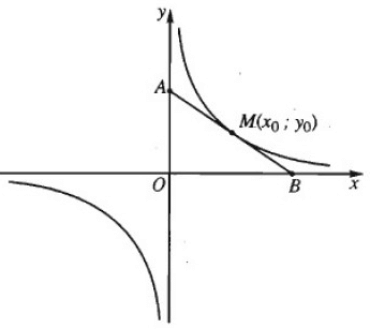
Phương trình tiếp tuyến tại M(x0; y0)M(x0; y0) là
Suy ra diện tích tam giác OAB là

Gọi A' và B' lần lượt là ảnh của A và B qua phép tịnh tiến \(\overrightarrow{u}\)
\(\Rightarrow A';B'\) đều thuộc d2
Theo công thức tọa độ ta có \(\left\{{}\begin{matrix}A'\left(-4;3\right)\\B'\left(0;5\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{A'B'}=\left(4;2\right)=2\left(2;1\right)\)
\(\Rightarrow\) Đường thẳng d2 nhận \(\left(1;-2\right)\) là 1 vppt
Phương trình d2:
\(1\left(x-0\right)-2\left(y-5\right)=0\Leftrightarrow x-2y+10=0\)