Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
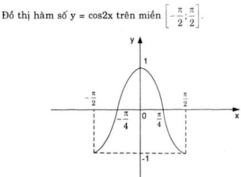
Từ đó suy ra
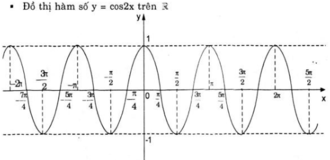
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
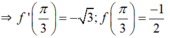
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
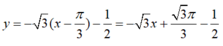
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
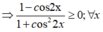
⇒ 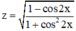 luôn xác định với mọi x ∈ R.
luôn xác định với mọi x ∈ R.

Ta biết rằng : sin x = sin ( x + k 2 π ) ; k ∈ Z
Do đó, nếu ta tịnh tiến đồ thị theo vecto u → = k 2 π ; k ∈ Z thì sẽ biến đồ thị đã cho thành chính nó .
Vì có vô số số nguyên k nên cũng có vô số phép tịnh tiến thỏa mãn đầu bài.
Đáp án D

a, Lấy đối xứng tất cả các điểm trên đồ thị y = sinx (trừ gốc tọa độ) qua trục tung ta được đồ thị y = - sinx
b, Giữ nguyên phần đồ thị nằm bên trái Oy.
Bỏ phần đồ thị bên phải
Lấy đối xứng đồ thị nằm bên trái Oy qua Oy
Đồ thị y = sin|x| là hợp của 2 phần ở trên
c, Tịnh tiến độ thị y = sinx theo vecto \(\overrightarrow{u}=\left(1;0\right)\), hay nói dễ hiểu hơn là dịch chuyển đồ thị y = sinx lên trên 1 đơn vị độ dài
ta được đồ thị y = sinx + 1

a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)

\(A\left(1;3\right)\) thuộc đths \(\Rightarrow a+b+c+1=3\Rightarrow a+b+c=2\) (1)
\(B\left(-1;4\right)\) thuộc đths \(\Rightarrow-a+b-c+1=4\Rightarrow-a+b-c=3\) (2)
Ta có \(y'\left(x\right)=3ax^2+2bx+c\)
\(y'\left(2\right)=0\Rightarrow12a+4b+c=0\) (3)
Từ (1), (2) và (3) ta được \(a=-\dfrac{19}{22};b=\dfrac{5}{2};c=\dfrac{4}{11}\)
Vậy hàm số đã cho là \(y=-\dfrac{19}{22}x^3+\dfrac{5}{2}x^2+\dfrac{4}{11}x+1\)

a, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)