NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
27 tháng 10 2017
1/
n=2 ta thấy đúng
GS đúng với n=k tức là (1-x)k+(1+x)k<2k
Ta cm đúng với n=k+1
(1-x)k+1+(1+x)k+1< (1-x)k+(1+x)k+(1-x)(1+x)k+(1-x)k(1+x)= 2\(\left(\left(1-x\right)^k+\left(1+x\right)^k\right)\)\(< 2.2^k=2^{k+1}\)
=> giả sử là đúng
theo nguyên lí quy nạp ta có đpcm
D
0
28 tháng 3 2019
\(f\left(x;y\right)=x+y+x\sqrt{1-y^2}+y\sqrt{1-x^2}\)
\(\Rightarrow\frac{\sqrt{3}}{2}f\left(x;y\right)=\frac{\sqrt{3}}{2}\left(x+y\right)+\frac{1}{2}\left(x\sqrt{3-3y^2}+y\sqrt{3-3x^2}\right)\)
\(\Rightarrow\frac{\sqrt{3}}{2}f\left(x;y\right)\le\frac{\frac{3}{4}+x^2+\frac{3}{4}+y^2}{2}+\frac{1}{2}\left(\frac{-3x^2+y^2+3-3y^2+x^2+3}{2}\right)\)
\(\Rightarrow\frac{\sqrt{3}}{2}f\left(x;y\right)\le\frac{\frac{3}{2}+x^2+y^2-x^2-y^2+3}{2}=\frac{9}{4}\)
\(\Rightarrow f\left(x;y\right)\le\frac{3\sqrt{3}}{2}\)
Dấu "=" khi x = y = \(\frac{\sqrt{3}}{2}\).
#Kaito#
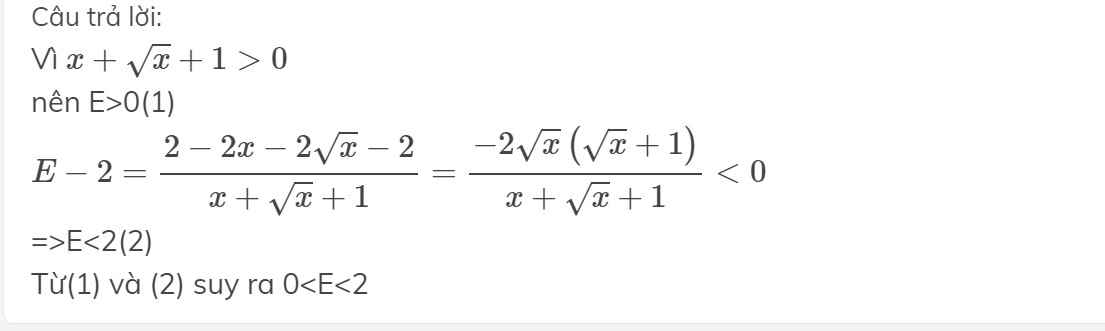
Vì \(x+\sqrt{x}+1>0\)
nên E>0(1)
\(E-2=\dfrac{2-2x-2\sqrt{x}-2}{x+\sqrt{x}+1}=\dfrac{-2\sqrt{x}\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}< 0\)
=>E<2(2)
Từ(1) và (2) suy ra 0<E<2