Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi (P) là mặt phẳng đi qua cạnh AB và song song với cạnh CD. Mặt phẳng (P) có vecto pháp tuyến n → vuông góc với hai vecto A B → = - 4 ; 5 ; - 1 v à C D → - 1 ; 0 ; 2
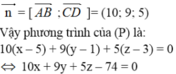

Mặt phẳng ( α ) đi qua điểm D và song song với mặt phẳng (ABC) nên ( α ) cũng có vecto pháp tuyến là n ' → = (1; 1; 1)
Vậy phương trình của ( α ) là: (x – 4) + (y) + (z – 6) = 0 hay x + y + z – 10 = 0.

Hai vecto có giá song song với mặt phẳng ( α ) là: u → = (0; 1; 1) và v → = (−1; 0; 2).
Suy ra ( α ) có vecto pháp tuyến là n → = u → ∧ v → = (2; −1; 1)
Mặt phẳng ( α ) đi qua điểm A(1; 0; 0) và nhận n → = (2; −1; 1) là vecto pháp tuyến. Vậy phương trình của (α) là: 2(x – 1) – y + z = 0 hay 2x – y + z – 2 = 0

\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{CD}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{CD}\right]=\left(-1;2;-1\right)=-\left(1;-2;1\right)\)
Phương trình (P):
\(1\left(x-1\right)-2y+1\left(z-1\right)=0\Leftrightarrow x-2y+z-2=0\)
Để tìm phương trình mặt phẳng (P) ta cần tìm được vector pháp tuyến của mặt phẳng. Vì mặt phẳng (P) song song với đường thẳng AB nên vector pháp tuyến của (P) cũng vuông góc với vector chỉ phương của AB, tức là AB(1-0;2-0;4-1)=(1;2;3).
Vì (P) đi qua C(1;0;1) nên ta dễ dàng tìm được phương trình của (P) bằng cách sử dụng công thức phương trình mặt phẳng:
3x - 2y - z + d = 0, trong đó d là vế tự do.
Để tìm d, ta chỉ cần thay vào phương trình trên cặp tọa độ (x;y;z) của điểm C(1;0;1):
3(1) -2(0) - (1) + d = 0
⇒ d = -2
Vậy phương trình của mặt phẳng (P) là:
3x - 2y - z - 2 = 0,
và đáp án là B.

Vì mặt phẳng (α) song song với mặt phẳng ( β) : 2x – y + 3z + 4 = 0 nên phương trình của mp(α) có dạng 2x – y + 3z + D = 0
Vì M(2; -1; 2) ∈ mp(α) nên 4 + 1 + 6 + D = 0 <=> D = -11
Vậy phương trình của mp(α) là: 2x – y + 3z - 11= 0

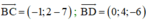
(BCD) nhận 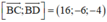 là 1 vtpt
là 1 vtpt
⇒ (BCD): 16x – 6y – 4z + 8 = 0
hay (BCD): 8x – 3y – 2z + 4 = 0.

Đáp án C
Phương trình mặt phẳng qua M và song song với ( α ) là:
3(x-3)-(y+1)+2(z+2)=0 ⇔ 3x-y+2z-6=0

Mặt phẳng ( β ) song song với trục Oy và vuông góc với mặt phẳng ( α ):
2x – y + 3z + 4 = 0, do đó hai vecto có giá song song hoặc nằm trên ( β ) là: j → = (0; 1; 0) và n α → = (2; −1; 3)
Suy ra ( β ) có vecto pháp tuyến là n β → = j → ∧ n α → = (3; 0; −2)
Mặt phẳng ( β ) đi qua điểm M(2; -1; 2) có vecto pháp tuyến là: n β → = (3; 0; −2)
Vậy phương trình của ( β ) là: 3(x – 2) – 2(z – 2) = 0 hay 3x – 2z – 2 = 0

(α) chứa AB và song song với CD
⇒ (α) nhận (1; 0; -1) là 1 vtpt
(α) đi qua A(-2; 6; 3)
⇒ (α): x – z + 5 = 0.