Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{GIẢI :}\)
A B C M E D
Chứng minh :
a) Xét \(\diamond\text{AEMD}\), có \(\hept{\begin{cases}\text{AE // DM }\\\text{EM // AD}\end{cases}}\)
\(\Rightarrow \text{ }\diamond\text{AEMD}\) là hình bình hành.
b) Để hình bình hành AEMD là hình thoi \(\Rightarrow\) AM là đường phân giác của góc A.
c) Để hình bình hành AEMD là hình vuông \(\Rightarrow\text{ }\hept{\begin{cases}\bigtriangleup\text{ABC vuông tại A}\\\text{AM là đường phân giác góc A}\end{cases}}\).

\(\text{GIẢI :}\)
A B C M D E
a) Xét \(\diamond\text{ADME}\) có \(DM\text{ }//\text{ }AB\), \(EM\text{ }//\text{ }AC\) \(\Rightarrow\text{ }\diamond\text{ADME}\) là hình bình hành.
b) Để hình bình hành ADME là hình thoi \(\Leftrightarrow\text{ }AM\) là tia phân giác của góc A.
Vậy M là giao điểm của tia phân giác góc A và cạnh BC thì ADME là hình thoi.
c) Để hình bình hành ADME là hình chữ nhật \(\Leftrightarrow\angle\text{A}=90^0\text{ }\Leftrightarrow\text{ }\bigtriangleup\text{ABC}\) vuông tại A.

bạn tự vẽ hình nk.
cm: vì m, n lần lượt là chân đg vuông góc kẻ từ d dến ab,ac
=> tứ giác AMDN là hình chữ nhật (có 3 góc vuông) (dh nb hcn)
mặt #: ad là đg phân giác của góc a
=> hcn AMDN là hình vuông vì có có đường chéo là đường phân giác của góc a(dh nb hv)

Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
mà AD là tia phân giác
nên AMDN là hình vuông

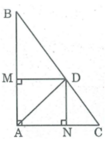
Xét tứ giác AMDN, ta có: ∠ (MAN) = 90 0 (gt)
DM ⊥ AB (gt)
⇒ ∠ (AMD) = 90 0
DN ⊥ AC (gt) ⇒ ∠ (AND) = 90 0
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông


\(\text{GIẢI :}\)
A B C D N M
Chứng minh :
Ta có : M là chân đường vuông góc kẻ từ A đến AB \(\Rightarrow\text{ }\widehat{\text{M}}=90^{\text{o}}\).
N là chân đường vuông góc kẻ từ A đến AC \(\Rightarrow\text{ }\widehat{\text{N}}=90^{\text{o}}\)
Xét \(\diamond\text{AMDN}\) có \(\widehat{\text{A}}=\widehat{\text{M}}=\widehat{\text{N}}=90^{\text{o}}\)\(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình chữ nhật.
mà AD là đường phân giác của góc A \(\Rightarrow\text{ }\diamond\text{AMDN}\) là hình vuông.