Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời................
Tớ không biết đúng hay sai đâu nha Ý Phạm
a,Xét tam giác ABE (BAE^ vuông) và tam giác HBE (BHE^ vuông) có:
BE=BE (cạnh chung)
ABE^=HBE^
⟹ ABE^=HBE^(ch+gn)
b,Ta có:
BA=BH (tam giác ABE = tam giác HBE)
EA=EH (________________________)
⟹ BE là đường trung trực của AH
c,Xét tam giác EKA và tam giác ECH có
AE=EH (gt)
EAK^=EHK^(=90o)
AEK^=HEC^(đối đỉnh)
⟹Tam giác EKA=tam giacsEHK (g-c-g)
⟹EK=EH ( cạnh tương ứng)
d,Từ điểm E đến đường thẳng HC có:
EH là đường vuông góc
EC là đường xiên
⟹EH<EC( quan hệ đường vuông góc)
Mà EH=AE(tam giác ABE = tam giác HBE)
⟹AE<AC

ABCI
a) Xét tam giác ABC và tam giác DMC có :
BC = CM ( GT )
Góc ACB = góc MCD ( 2 góc đối đỉnh (
AC = CD ( GT )
=> tam giác ABC = tam giác DMC ( c - g - c )
b) Theo ý a , ta có : tam giác ABC = tam giác DMC
=> Góc BAD = góc ADM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> MD // AB ( dấu hiệu )
c) Nghĩ nốt đã

B A E M K C H
a) Bạn ghi câu a) không rõ ràng nên mình thay thế bằng ý kiến của mình nhé !
CMR : \(\Delta ABE=\Delta HBE\)
Xét \(\Delta ABE,\Delta HBE\) có :
\(BA=BH\left(gt\right)\)
\(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác của \(\widehat{B}\) )
\(BE:chung\)
=> \(\Delta ABE=\Delta HBE\left(c.g.c\right)\)
b) Gọi \(AH\cap BE=\left\{O\right\};O\in BE\)
Xét \(\Delta ABO,\Delta HBO\) có :
\(AB=BH\left(gt\right)\)
\(\widehat{ABO}=\widehat{HBO}\) (BE là tia phân giác của \(\widehat{B}\) ; \(O\in BE\))
AO : Chung
=> \(\Delta ABO=\Delta HBO\left(c.g.c\right)\)
=> \(\widehat{BOA}=\widehat{BOH}\) (2 góc tương ứng)
Mà : \(\widehat{BOA}+\widehat{BOH}=180^o\left(Kềbù\right)\)
=> \(\widehat{BOA}=\widehat{BOH}=\dfrac{180^o}{2}=90^o\)
=> \(BO\perp AH\)
Hay : \(BE\perp AH\)
c) Ta chứng minh được : \(\Delta BKE=\Delta BCE\)
Suy ra : \(EK=EC\) (2 cạnh tương ứng)
d) Xét \(\Delta ABC\) có :
BE là tia phân giác của \(\widehat{ABC}\) (1)
Xét \(\Delta KEM,\Delta CEM\) có :
\(EK=EC\left(cmt\right)\)
\(EM:chung\)
\(KM=CM\) (M là trung điểm của KC)
=> \(\Delta KEM=\Delta CEM\left(c.c.c\right)\)
=> \(\widehat{MEK}=\widehat{MEC}\) (2 góc tương ứng)
=> EM là tia phân giác của \(\widehat{KEC}\) (2)
Từ (1) và (2) => \(BE\equiv ME\)
=> B, E, M thẳng hàng
=> đpcm.
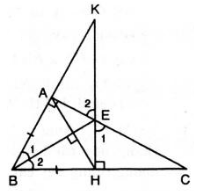


a) Xét \(\Delta BAE\) và \(\Delta BHE\) có:
-\(\widehat{BAE}=\widehat{BHE}=90^0\)(gt)
-BE chung
-\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta HBE\) (cạnh huyền-góc nhọn) (đpcm)
b) Ta có:
-AB=HB (do \(\Delta ABE=\Delta HBE\)) nên B thuộc đường trung trực của AH (1)
-EA=EH (do \(\Delta ABE=\Delta HBE\)) nên E thuộc đường trung trực của AH (2)
Từ (1) và (2), ta có: BE là đường trung trực của AH (đpcm)
c) Ta có:
\(\widehat{BEC}\) là góc ngoài của \(\Delta BEA\)
\(\Rightarrow\) \(\widehat{BEC}\) = \(\widehat{BAE}+\widehat{ABE}\)
\(\Rightarrow\widehat{BEC}=90^0+\widehat{ABE}\)
\(\Rightarrow\widehat{BEC}>90^0\)
Trong \(\Delta BEC\) có: \(\widehat{BEC}\) là góc lớn nhất nên BC là cạnh lớn nhất (quan hệ góc và cạnh đối diện của tam giác) hay BC>BE \(\Rightarrow\)AC>AE (quan hệ đường xiên-hình chiếu) (đpcm)
d) Xét \(\Delta AEK\) và \(\Delta HEC\) có:
-\(\widehat{KAE}=\widehat{EHC}=90^0\)
-EA=HE (câu a)
-\(\widehat{AEK}=\widehat{HEC}\) (đối đỉnh)
=> \(\Delta AEK=\Delta HEC\) (cạnh góc vuông-góc nhọn kề)
=> AK=HC (2 cạnh tương ứng)
Ta có:
BA=BH và AK=HC
=> BA+AK=BH+HC
=> BK=BC
Xét \(\Delta BKI\) và \(\Delta BCI\):
-BK=BC (cmt)
-KI=IC (gt)
-BI chung
=> \(\Delta BKI=\Delta BCI\left(c.c.c\right)\)
=> \(\widehat{KBI}=\widehat{CBI}\) (2 góc tương ứng)
=> BI là phân giác của \(\widehat{ABC}\)
Mà BE cũng là phân giác của \(\widehat{ABC}\)
=>BI\(\equiv\)BE hay B,E,I thẳng hàng (đpcm)
A B C E H K I