Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) (2;-5)
(0;-2)
2) (1;0) / (6;1)
3) (3;-2) / (0;-2)
4) (3;-2)

Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
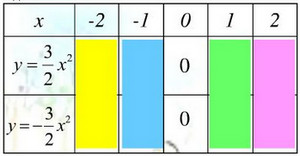
Vẽ đồ thị:
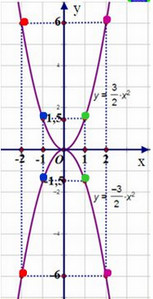
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO

a)
Với y = -1/2x + 3, ta có f(-2,5) = -1/2(-2,5) + 3 = (2,5 + 6)/2 = 4,25;
Tương tự: f(-2) = 4; f(-1,5) = 3,75 ; f(-1) = 3,5 ; f(-0,5) = 3,25; f(0) = 3; f(0,5) = 2,75; f(1) = 2,5 ; f(1,5) = 2,25 ; f(2) = 2 ; f(2,5) = 1,75.

b) Hàm số nghịch biến vì khi x tăng lên thì y giảm đi.
Xem thêm tại: http://loigiaihay.com/bai-2-trang-45-sgk-toan-9-tap-1-c44a4307.html#ixzz4ezVwgGJL

\(\sqrt{4x^2-4x+1}=\sqrt{x^2+10x+25}\left(x\ge\frac{1}{2}\right)\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+5\right)^2}\)
\(\Leftrightarrow2x-1=x+5\)
\(\Leftrightarrow2x-1-x-5=0\)
\(\Leftrightarrow x-6=0\Leftrightarrow x=6\left(tm\right)\)
vậy x=6 là nghiệm của phương trình
b) \(\sqrt{x+3}+2\sqrt{4x+12}-\frac{1}{3}\sqrt{9x+27}=8\left(x\ge-3\right)\)
\(\Leftrightarrow\sqrt{x+3}+2\sqrt{4\left(x+3\right)}-\frac{1}{3}\sqrt{9\left(x+3\right)}=8\)
\(\Leftrightarrow\sqrt{x+3}+4\sqrt{x+3}-\sqrt{x+3}=8\)
\(\Leftrightarrow4\sqrt{x+3}=8\)
\(\Leftrightarrow x+3=4\)
<=> x=-1 (tmđk)
vậy x=-1 là nghiệm của phương trình

a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
b)Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là hai đơn vị.
a) Giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x :

b) Khi x lấy cùng một giá trị thì giá trị của hàm số y = 0,5x + 2 lớn hơn giá trị của hàm số y = 0,5x là 2 đơn vị.

Để là phân tích thành nhân tử chứ nhỉ?? Chẳng lẽ là "Phân tích ra thừa số nguyên tố" ![]()
ĐK: \(x\ge0\)
Đặt \(\sqrt{x}=t\) cho dễ nhìn
a) \(t^2-5t+6=t^2-3t-2t+6\)
\(=t\left(t-3\right)-2\left(t-3\right)=\left(t-3\right)\left(t-2\right)=\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)\)
b) \(t^2-t-2=t^2+t-2t-2=t\left(t+1\right)-2\left(t+1\right)\)
\(=\left(t+1\right)\left(t-2\right)=\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)\)
Cảm ơn bạn nhiều nhaaaaa <3 mình xem mấy cái đáp án khác làm tắt không hiểu j ^^ cảm ơn bạn đã làm từng bước để mình hiểu <3 cảm ơn bạn nhiều nhaaaa

a) Hpt có nghiệm duy nhất khi \(m\ne3;m\ne4\)
Hpt có vô số nghiệm khi \(\hept{\begin{cases}m=3\\m=4\end{cases}}\)(vô lí). Vậy hệ không thể có vô số nghiệm
b) \(\hept{\begin{cases}3x+my=4\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}3\left(1-y\right)+my=4\\x=1-y\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m-3\right)y=1\\x=1-y\end{cases}}\)
\(\cdot m=3\Rightarrow\hept{\begin{cases}0=1\\x=1-y\end{cases}}\)(vô lí)
\(\cdot m>3\Rightarrow\hept{\begin{cases}y=\frac{1}{m-3}>0\\x=1-\frac{1}{m-3}=\frac{m-4}{m-3}\end{cases}}\)
Để \(x< 0\)thì \(\frac{m-4}{m-3}< 0\). Mà \(m-3>0\Leftrightarrow m>3\)nên \(m-4< 0\Leftrightarrow m< 4\)
\(\Rightarrow3< m< 4\)
\(\cdot m< 3\Rightarrow\hept{\begin{cases}y=\frac{1}{m-3}< 0\\x=1-\frac{1}{m-3}=\frac{m-4}{m-3}\end{cases}}\)(loại do \(y< 0\))
Vậy \(3< m< 4\)thì thỏa ycbt




a) \(M=\left(\dfrac{3}{\sqrt{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt{x}-5}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{3.\left(\sqrt{x}-3\right)+x+9}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-5-\left(\sqrt{x}-3\right)}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+3\sqrt{x}}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-2}{\sqrt{x}.\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}.\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}.\left(\sqrt{x}-3\right)}{\sqrt{x}-2}=\dfrac{x}{\sqrt{x}-2}\)
b) \(M< 0\Leftrightarrow\sqrt{x}-2< 0\Leftrightarrow x< 4\)
Kết hợp điều kiện ta được \(0< x< 4\) thì M < 0
c) Từ câu b ta có M < 0 \(\Leftrightarrow0< x< 4\)
nên \(x\inℤ\) để M nguyên âm <=> \(x\in\left\{1;2;3\right\}\)
Thay lần lượt các giá trị vào M được x = 1 thỏa
d) \(M=\dfrac{x}{\sqrt{x}-2}=\sqrt{x}+2+\dfrac{4}{\sqrt{x}-2}=\left(\sqrt{x}-2+\dfrac{4}{\sqrt{x}-2}\right)+4\)
Vì x > 4 nên \(\sqrt{x}-2>0\)
Áp dụng BĐT Cauchy ta có
\(M=\left(\sqrt{x}-2+\dfrac{4}{\sqrt{x}-2}\right)+4\ge2\sqrt{\left(\sqrt{x}-2\right).\dfrac{4}{\sqrt{x}-2}}+4=8\)
Dấu "=" xảy ra khi \(\sqrt{x}-2=\dfrac{4}{\sqrt{x}-2}\Leftrightarrow x=16\left(tm\right)\)
1) \(M=\left(\dfrac{3}{\sqrt[]{x}+3}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5}{x-3\sqrt[]{x}}-\dfrac{1}{\sqrt[]{x}}\right)\left(x>0;x\ne9\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\left(\sqrt[]{x}-3\right)}{\left(\sqrt[]{x}+3\right)\left(\sqrt[]{x}-3\right)}+\dfrac{x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}-\dfrac{1}{\sqrt[]{x}}\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\sqrt[]{x}-9+x+9}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5-\left(\sqrt[]{x}-3\right)}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{3\sqrt[]{x}+x}{x-9}\right):\left(\dfrac{2\sqrt[]{x}-5-\sqrt[]{x}+3}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{\sqrt[]{x}\left(\sqrt[]{x}+3\right)}{x-9}\right):\left(\dfrac{\sqrt[]{x}-2}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\left(\dfrac{\sqrt[]{x}}{\sqrt[]{x}-3}\right):\left(\dfrac{\sqrt[]{x}-2}{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}\right)\)
\(\Leftrightarrow M=\dfrac{\sqrt[]{x}}{\sqrt[]{x}-3}.\dfrac{\sqrt[]{x}\left(\sqrt[]{x}-3\right)}{\sqrt[]{x}-2}\)
\(\Leftrightarrow M=\dfrac{x}{\sqrt[]{x}-2}\)
2) Để \(M< 0\) khi và chỉ chi
\(M=\dfrac{x}{\sqrt[]{x}-2}< 0\left(1\right)\)
Nghiệm của tử là \(x=0\)
Nghiệm của mẫu \(\sqrt[]{x}-2=0\Leftrightarrow\sqrt[]{x}=2\Leftrightarrow x=4\)
Lập bảng xét dấu... ta được
\(\left(1\right)\Leftrightarrow0< x< 4\)