
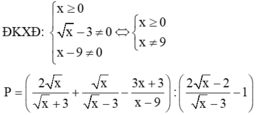
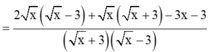
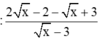
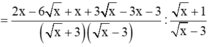
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

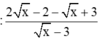
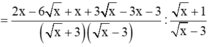
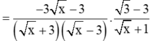
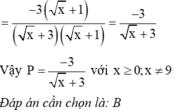

Mình ghi nhầm. \(x=\frac{\sqrt{4+2\sqrt{3}}.\left(\sqrt{3}-1\right)}{\sqrt{6+2\sqrt{5}}-\sqrt{5}}\)nhé

\(a)\)\(R=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3\left(\sqrt{x}+3\right)}{x-9}\right):\left(\frac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
\(R=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(R=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3}{\sqrt{x-3}}\right):\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(R=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}-3}{\sqrt{x}-3}\right):\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(R=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+1\right):\frac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(R=\frac{3\sqrt{x}+3}{\sqrt{x}+3}.\frac{\sqrt{x}-3}{\sqrt{x+1}}\)
\(R=\frac{3\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}\)
\(R=\frac{3\left(\sqrt{x}-3\right)}{\sqrt{x}+3}\)
\(b)\) Ta có : \(R< -1\)
\(\Leftrightarrow\)\(\frac{3\left(\sqrt{x}-3\right)}{\sqrt{x}+3}< -1\)
\(\Leftrightarrow\)\(\frac{\sqrt{x}-3}{\sqrt{x}+3}< \frac{-1}{3}\)
\(\Leftrightarrow\)\(3\sqrt{x}-9< -\sqrt{x}-3\)
\(\Leftrightarrow\)\(4\sqrt{x}< 6\)
\(\Leftrightarrow\)\(\sqrt{x}< \frac{3}{2}\)
\(\Leftrightarrow\)\(x< \frac{9}{4}\)
Chúc bạn học tốt ~

a) \(A=\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}+1}{\sqrt{x}-3}+\frac{3-11\sqrt{x}}{9-x}=\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}+1}{\sqrt{x}-3}+\frac{11\sqrt{x}-3}{x-9}=\frac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\frac{2x-6\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{x+4\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\frac{2x-6\sqrt{x}+x+4\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\frac{3x+9\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\frac{3\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\frac{3\sqrt{x}}{\sqrt{x}-3}\)

P/s : sửa đề
ĐKXĐ : \(\hept{\begin{cases}x\ge0\\x\ne9\end{cases}}\)
a) \(P=\left(\frac{2\sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{3x+3}{x-9}\right):\left(\frac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
\(P=\frac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\frac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)
\(P=\frac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{x-9}.\frac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(P=\frac{-3\sqrt{x}-3x}{x-9}.\frac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(P=\frac{-3\sqrt{x}\left(1+\sqrt{x}\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}\)
\(P=\frac{-3\sqrt{x}}{\sqrt{x}+3}\)
b) \(P< -\frac{1}{2}\)
\(\Leftrightarrow\frac{-3\sqrt{x}}{\sqrt{x}+3}+\frac{1}{2}< 0\)
\(\Leftrightarrow\frac{-6\sqrt{x}+\sqrt{x}+3}{2\left(\sqrt{x}+3\right)}< 0\)
\(\Leftrightarrow\frac{-5\sqrt{x}+3}{2\left(\sqrt{x}+3\right)}< 0\)
Mà \(2\left(\sqrt{x}+3\right)>0\)
\(\Rightarrow-5\sqrt{x}+3< 0\)
\(\Leftrightarrow-5\sqrt{x}< -3\)
\(\Leftrightarrow\sqrt{x}>\frac{3}{5}\)
\(\Leftrightarrow x>\frac{9}{25}\)
Vấy .................
c) \(P.\left(\sqrt{x}+3\right)+2\sqrt{x}-2+x=2\)
\(\Leftrightarrow\frac{-3\sqrt{x}}{\sqrt{x}+3}\left(\sqrt{x}+3\right)+2\sqrt{x}-2+x=2\)
\(\Leftrightarrow-3\sqrt{x}+2\sqrt{x}-2-2+x=0\)
\(\Leftrightarrow-\sqrt{x}-4+x=0\)
\(\Leftrightarrow-\sqrt{x}\left(1-\sqrt{x}\right)=4\)
Còn lại lập bảng tự tìm giá trị của x là ra .( Chú ý : đối chiếu ĐKXĐ )
d)
\(P.\left(\sqrt{x}+3\right)+x\left(\sqrt{x}-m\right)=x-\sqrt{x}\left(3+m\right)\)
\(\Leftrightarrow\frac{-3\sqrt{x}}{\sqrt{x}+3}\left(\sqrt{x}+3\right)+x\sqrt{x}-xm=x-3\sqrt{x}-m\sqrt{x}\)
\(\Leftrightarrow-3\sqrt{x}+x\sqrt{x}-xm-x+3\sqrt{x}+m\sqrt{x}=0\)
\(\Leftrightarrow\sqrt{x}\left(x+m\right)-x\left(m+1\right)=0\)
\(\Leftrightarrow\sqrt{x}\left[x+m-m\sqrt{x}-\sqrt{x}\right]=0\)
\(\Leftrightarrow\sqrt{x}\left[m\left(1-\sqrt{x}\right)-\sqrt{x}\left(1-\sqrt{x}\right)\right]=0\)
\(\Leftrightarrow\sqrt{x}=0;m-\sqrt{x}=0;1-\sqrt{x}=0\)
+) \(\sqrt{x}=0\Leftrightarrow x=0\left(TM\right)\)
+) \(1-\sqrt{x}=0\)
\(\Leftrightarrow x=1\left(TM\right)\)
+) \(m-\sqrt{x}=0\)
\(\Leftrightarrow\orbr{\begin{cases}m-\sqrt{0}=0\\m-\sqrt{1}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}m=0\\m=1\end{cases}}}\)
Vậy ..................