Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 :
a ) \(\sqrt{0,36.100}=\sqrt{36}=6\)
b ) \(\sqrt[3]{-0,008}=\sqrt[3]{\left(-0,2\right)^3}=-0,2\)
c ) \(\sqrt{12}+6\sqrt{3}+\sqrt{27}=2\sqrt{3}+6\sqrt{3}+3\sqrt{3}=11\sqrt{3}\)
Câu 2 :
a ) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}=a-\sqrt{ab}+b\)

a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.
a) ĐS: .
b) ĐS: Nếu thì
Nếu ab
c) ĐS:
d)
Nhận xét. Nhận thấy rằng để có nghĩa thì
Do đó
. Vì thế có thể phân tích tử thành nhân tử.

a: \(=4\left|a-3\right|=4\left(a-3\right)=4a-12\)
b: \(=9\cdot\left|a-9\right|=9\left(9-a\right)=81-9a\)
c: \(a^3b^6\cdot\sqrt{\dfrac{3}{a^6b^4}}=a^3b^6\cdot\dfrac{\sqrt{3}}{-a^3b^2}=-b^4\sqrt{3}\)
d: \(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{a-b}\)
\(=\dfrac{a+\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}\)

bài 2 ) a) đk : \(a>0;b>0\)
b) P = \(\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}\)
P = \(\dfrac{a-2\sqrt{ab}+b+4\sqrt{ab}}{\sqrt{a}+\sqrt{b}}.\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{ab}}\)
P = \(\dfrac{a+2\sqrt{ab}+b}{\sqrt{a}+\sqrt{b}}.\sqrt{a}-\sqrt{b}\) = \(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{a}+\sqrt{b}}.\sqrt{a}-\sqrt{b}\) = \(\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)\) = \(a-b\)
c) ta có P = \(a-b\) thay \(a=2\sqrt{3};b=\sqrt{3}\) vào ta có
P = \(2\sqrt{3}-\sqrt{3}=\sqrt{3}\) vậy khi \(a=2\sqrt{3};b=\sqrt{3}\) thì P = \(\sqrt{3}\)
bài 1) a) P = \(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}-1}{\sqrt{a}+1}\right)\)
P = \(\dfrac{\left(a\sqrt{a}-1\right)\left(a+\sqrt{a}\right)-\left(a\sqrt{a}+1\right)\left(a-\sqrt{a}\right)}{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}+\dfrac{a-1}{\sqrt{a}}.\dfrac{\left(\sqrt{a}+1\right)^2+\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
P = \(\dfrac{a^2\sqrt{a}+a^2-a-\sqrt{a}-\left(a^2\sqrt{a}-a^2+a-\sqrt{a}\right)}{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}+\dfrac{a-1}{\sqrt{a}}.\dfrac{a+2\sqrt{a}+1+a-2\sqrt{a}+1}{a-1}\)
P = \(\dfrac{a^2\sqrt{a}+a^2-a-\sqrt{a}-a^2\sqrt{a}+a^2-a+\sqrt{a}}{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}+\dfrac{2a+2}{\sqrt{a}}\)
P = \(\dfrac{2a^2-2a}{a^2-a}+\dfrac{2a+1}{\sqrt{a}}\) = \(\dfrac{2\left(a^2-a\right)}{a^2-a}+\dfrac{2a+2}{\sqrt{a}}\)
P = \(2+\dfrac{2a+2}{\sqrt{a}}\) = \(\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}\)
b) ta có P = 7 \(\Leftrightarrow\) \(\dfrac{2a+2\sqrt{a}+2}{\sqrt{a}}=7\) \(\Leftrightarrow\) \(2a+2\sqrt{a}+2=7\sqrt{a}\)
\(\Leftrightarrow\) \(2a-5\sqrt{a}+2=0\) (1)
đặc \(\sqrt{a}=u\) \(\left(u\ge0\right)\) (1) \(\Leftrightarrow\) \(2u^2-5u+2\)
\(\Delta=\left(-5\right)^2-4.2.2\) = \(25-16=9>0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(u_1=\dfrac{5+3}{4}=\dfrac{8}{4}=2\left(tmđk\right)\)
\(u_2=\dfrac{5-3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\left(tmđk\right)\)
ta có : \(u=\sqrt{a}=2\Leftrightarrow x=4\)
\(u=\sqrt{a}=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{4}\)
vậy \(a=4;a=\dfrac{1}{4}\) thì P = 7

Bài 6:
a: \(\Leftrightarrow\sqrt{x^2+4}=\sqrt{12}\)
=>x^2+4=12
=>x^2=8
=>\(x=\pm2\sqrt{2}\)
b: \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>x+1=1
=>x=0
c: \(\Leftrightarrow3\sqrt{2x}+10\sqrt{2x}-3\sqrt{2x}-20=0\)
=>\(\sqrt{2x}=2\)
=>2x=4
=>x=2
d: \(\Leftrightarrow2\left|x+2\right|=8\)
=>x+2=4 hoặcx+2=-4
=>x=-6 hoặc x=2

ĐKXĐ : \(\left\{{}\begin{matrix}a,b\ge0\\a.b\ne1\end{matrix}\right.\)
a ) \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)+\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)-\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)-\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)+\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}.\dfrac{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{-2\sqrt{a}-2}=-\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{2\left(\sqrt{a}+1\right)}=-\sqrt{ab}\)
Câu b : Ta có : \(b=\dfrac{\sqrt{3}-1}{1+\sqrt{3}}=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}=\dfrac{3-2\sqrt{3}+1}{2}=2-\sqrt{3}\)
\(P=-\sqrt{ab}=-\sqrt{\left(2-\sqrt{3}\right)^2}=-\left|2-\sqrt{3}\right|=\sqrt{3}-2\)
Câu c : \(\sqrt{a}+\sqrt{b}=4\Rightarrow\sqrt{a}=4-\sqrt{b}\)
\(P=-\sqrt{ab}=-\left(4-\sqrt{b}\right)\sqrt{b}=b-4\sqrt{b}=\left(\sqrt{b}-2\right)^2-4\ge-4\)
Vậy GTNN của P là -4 . Dấu bằng xảy ra khi \(a=b=4\)

Bài 1:
a: \(=\sqrt{7}-2+2=\sqrt{7}\)
b: \(=\left(5\sqrt{5}-3\sqrt{3}\right)\cdot\dfrac{\sqrt{5}+\sqrt{3}}{8+\sqrt{15}}\)
\(=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)\cdot\left(8+\sqrt{15}\right)\cdot\left(\sqrt{5}+\sqrt{3}\right)}{8+\sqrt{15}}\)
=5-3=2

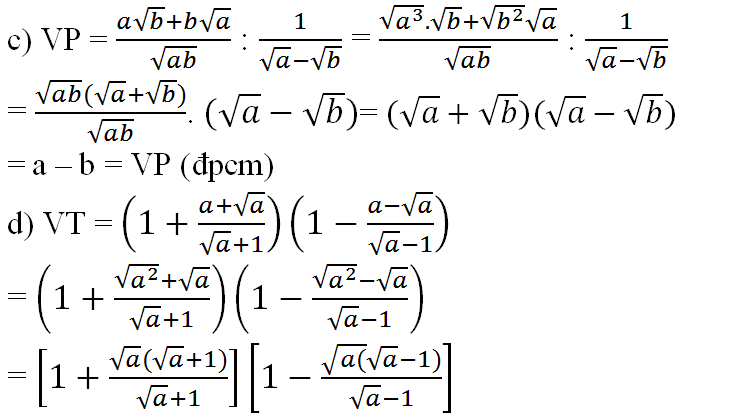


a: \(A=\dfrac{a-\sqrt{ab}-a}{a-b}:\dfrac{a+\sqrt{ab}-a}{\left(\sqrt{a}+\sqrt{b}\right)^2}\)
\(=\dfrac{-\sqrt{ab}}{a-b}\cdot\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\sqrt{ab}}=\dfrac{-\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
b: Khi a=7-4 căn 3 và b=7+4 căn 3 thì
\(A=\dfrac{-\left(2-\sqrt{3}+2+\sqrt{3}\right)}{2-\sqrt{3}-2-\sqrt{3}}=\dfrac{-4}{-2\sqrt{3}}=\dfrac{2}{\sqrt{3}}\)