Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A = [2t2(m - 1) - t(m - 1)(2t - 1)] + t + m
A = t(m - 1)[2t - (2t - 1)] + t + m
A = t(m - 1) + t + m
A = tm + m
b) Với m = 2; A = 0 thì ta được pt:
0 = 2t + 2
⇔ t = -1
Vậy khi m = 2 và để A = 0 thì t = -1

a) \(A=2t^2\left(m-1\right)-t\left(m-1\right)\left(2t-1\right)+t+m\)
\(A=2t^2m-2t^2-2t^2m+tm+2t^2-t+t+m\)
\(A=tm+m\)
b) Ta có:
\(t.2+2=0\)
\(\Leftrightarrow2t+2=0\)
\(\Leftrightarrow2t=-2\)
\(\Leftrightarrow t=-1\)
vậy: phương trình có tập nghiệm là: S = {-1}
t không chắc :v

Lời giải:
Áp dụng BĐT Cauchy cho các số không âm ta có:
\(\frac{2}{3}x^2+\frac{2}{3}y^2\geq 2.\sqrt{\frac{2}{3}x^2.\frac{2}{3}y^2}=2|\frac{2}{3}xy|\geq \frac{4}{3}xy\)
\(\frac{1}{3}x^2+\frac{4}{3}t^2\geq 2|\frac{2}{3}xt|\geq \frac{4}{3}xt\)
\(\frac{1}{3}y^2+\frac{4}{3}z^2\geq 2|\frac{2}{3}yz|\geq \frac{4}{3}yz\)
\(\frac{2}{3}z^2+\frac{2}{3}t^2\geq 2|\frac{2}{3}zt|\geq \frac{4}{3}zt\)
Cộng theo vế và rút gọn:
\(\Rightarrow x^2+y^2+2z^2+2t^2\geq \frac{4}{3}(xy+xt+yz+zt)\)
\(\Leftrightarrow 1\geq \frac{4}{3}(x+z)(y+t)\)
\(\Leftrightarrow A=(x+z)(y+t)\leq \frac{3}{4}\)
Vậy \(A_{\max}=\frac{3}{4}\)

Bài 2:
a: \(M=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2\left(x-5\right)\left(x+5\right)+50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+50-5x+2x^2-50}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)
b: Khi x=3 thì \(M=\dfrac{3-1}{2}=\dfrac{2}{2}=1\)
Khi x=5 thì \(M=\dfrac{5-1}{2}=\dfrac{4}{2}=2\)

a: ĐKXĐ: \(x\in\left\{0;\dfrac{1}{2}\right\}\)
b: \(A=\left(\dfrac{1}{x-1}-\dfrac{2x}{x^3-x^2+x-1}\right):\dfrac{1-2x}{x^2+1}\)
\(=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\cdot\dfrac{x^2+1}{1-2x}=\dfrac{x-1}{1-2x}\)
c: Để A>0 thì \(\dfrac{x-1}{2x-1}< 0\)
=>1/2<x<1

a: \(A=\dfrac{3x^2-4+2\left(x+1\right)-2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{x+1}{x+1-x}\)
\(=\dfrac{3x^2-4+2x+2-2x+2}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{x+1}{1}\)
\(=\dfrac{3x^2}{\left(x+1\right)\left(x-1\right)}\cdot\dfrac{x+1}{1}=\dfrac{3x^2}{x-1}\)
b: Để A chia hết cho 2013 thì A=2013k
=>3x2=2013k(x-1)(k∈Z)

1. \(M=\left(\frac{1}{a}+\frac{a}{a+1}\right):\frac{a}{a^2+a}\) \(\left(a\ne0,a\ne-1\right)\)
\(=\frac{a+1+a^2}{a\left(a+1\right)}.\frac{a\left(a+1\right)}{a}=\frac{a^2+a+1}{a}\)
\(2.\left(a-5\right)\left(a+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-5=0\\a+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=5\left(t/m\right)\\a=-1\left(loai\right)\end{matrix}\right.\)
Với a = 5 thì \(M=\frac{5^2+5+1}{5}=\frac{31}{5}\)
3. \(M=\frac{a^2+a+1}{a}=a+1+\frac{1}{a}\)
a> 0 => 1/a >0
Áp dụng BĐT cô si với hai số a và \(\frac{1}{a}\) , có:
\(a+\frac{1}{a}\ge2\sqrt{a.\frac{1}{a}}=2\)
\(\Leftrightarrow a+1+\frac{1}{a}\ge3\)
Dấu = xảy ra \(\Leftrightarrow a=\frac{1}{a}\Leftrightarrow a^2=1\Leftrightarrow a=1\) ( vì a > 0)
Vậy \(Min_M=3\Leftrightarrow a=1\)
1. Rút gọn biểu thức M.
\(M=\left(\frac{1}{a}+\frac{a}{a}+1\right):\frac{a}{a^2}+a\)
\(M=\left(\frac{1}{a}+1+1\right):\frac{1}{a}+a\)
\(M=\left(\frac{1}{a}+2\right).a+a\)
\(M=\left(\frac{1}{a}+\frac{2a}{a}\right).a+a\)
\(M=\frac{2a+1}{a}.a+a\)
\(M=\frac{a.\left(2a+1\right)}{a}+a\)
\(M=2a+1+a\)
\(M=3a+1\)
( HS 6->7 làm bài )
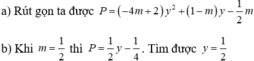
\(=2t^2m-2t^2-t\left(2tm-m-2t+1\right)+t+m\)
\(=2t^2m-2t^2-2t^2m+tm+2t^2-t+t+m\)
=tm+m