Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
AB′ABAB′AB = AC′ACAC′AC => ACAC′ACAC′ = ABAB′ABAB′
=> ACAC′ACAC′ - 1 = AC−AC′AC′AC−AC′AC′ = AB−AB′AB′AB−AB′AB′
=> CC′AC′CC′AC′<...
a) Ta có:
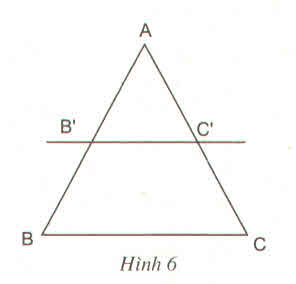
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\Rightarrow\dfrac{AB}{AC}=\dfrac{AB'}{AC'}\)
Áp dụng tc dãy tỉ số bằng nhau ta có;
\(\dfrac{AB}{AC}=\dfrac{AB'}{AC'}=\dfrac{AB-AB'}{AC-AC'}=\dfrac{BB'}{CC'}\)
\(\Rightarrow\dfrac{AB'}{AC'}=\dfrac{BB'}{CC'}\Leftrightarrow\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)
b) Ta có:
\(\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\left(cmt\right)\)
\(\Leftrightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Leftrightarrow\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)

Bài 2:
a: Gọi I là trung điểm của MC
Ta có: \(MI=IC=\dfrac{MC}{2}\)
\(AM=\dfrac{MC}{2}\)
Do đó: AM=MI=IC
=>AM=MI
=>M là trung điểm của AI
Xét ΔBMC có
D,I lần lượt là trung điểm của CB,CM
=>DI là đường trung bình của ΔBMC
=>DI//BM và \(DI=\dfrac{BM}{2}\)
DI//BM
O\(\in\)BM
Do đó: DI//OM
Xét ΔADI có
M là trung điểm của AI
MO//DI
Do đó: O là trung điểm của AD
b: Xét ΔADI có O,M lần lượt là trung điểm của AD,AI
=>OM là đường trung bình của ΔADI
=>\(OM=\dfrac{1}{2}DI=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BM=\dfrac{1}{4}BM\)
Bài 1:
a: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
=>\(\dfrac{AB}{AB'}=\dfrac{AC}{AC'}\)
=>\(\dfrac{AB-AB'}{AB'}=\dfrac{AC-AC'}{AC'}\)
=>\(\dfrac{BB'}{AB'}=\dfrac{CC'}{AC'}\)
=>\(\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)
b: Ta có: \(\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)
=>\(\dfrac{AB'+BB'}{BB'}=\dfrac{AC'+CC'}{CC'}\)
=>\(\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\)
=>\(\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)

Bạn đọc tự vẽ hình.
Xét tam giác \(AA'C\)có \(M,B,B'\)lần lượt nằm trên các cạnh \(AA',A'C,CA\)và \(M,B,B'\)thẳng hàng, do đó theo định lí Menelaus ta có:
\(\frac{MA}{MA'}.\frac{BA'}{BC}.\frac{B'C}{B'A}=1\Leftrightarrow\frac{MA}{MA'}.\frac{BA'}{BC}=\frac{B'A}{B'C}\)
Tương tự khi xét tam giác \(AA'B\)với các điểm \(M,B,B'\)ta cũng có:
\(\frac{MA}{MA'}.\frac{CA'}{CB}=\frac{C'A}{C'B}\)
Suy ra \(\frac{B'A}{B'C}+\frac{C'A}{C'B}=\frac{MA}{MA'}\left(\frac{BA'}{BC}+\frac{CA'}{CB}\right)=\frac{MA}{MA'}.\frac{BC}{BC}=\frac{MA}{MA'}\).
Ta có đpcm.
A' M B C C' B' D A E
\(\frac{AM}{A'M}=\frac{AE}{BA'}=\frac{AD}{A'C}=\frac{AD+AE}{A'C+A'B}=\frac{DE}{BC}\)
\(\Delta CBB'\)có AE // BC , nên \(\frac{AB'}{B'C}=\frac{AE}{BC}\)( hệ quả của định lí Ta-lét);
\(\Delta BCC'\)có DA // BC , nên \(\frac{AC'}{BC'}=\frac{DA}{BC}\)( hệ quả của định lí Ta-lét).
Ta có : \(\frac{AB'}{CB'}=\frac{AC'}{BC'}=\frac{AE}{BC}+\frac{DA}{BC}=\frac{DE}{BC}\)
Do đó : \(\frac{AM}{A'M}=\frac{AB'}{CB'}+\frac{AC'}{BC'}\)

a: Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=225\)
=>k=3
=>AB=9cm; AC=12cm
b: Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
=>25k2=1252
=>k=25
=>AB=75cm; AC=100cm

\(A=\sum\sqrt{\dfrac{ab}{c+ab}}=\sum\sqrt{\dfrac{ab}{c^2+ca+cb+ab}}\)
\(=\sum\sqrt{\dfrac{ab}{\left(c+a\right)\left(c+b\right)}}\le\dfrac{1}{2}\left(\dfrac{a}{c+a}+\dfrac{b}{c+b}+\dfrac{b}{a+b}+\dfrac{c}{a+c}+\dfrac{a}{b+a}+\dfrac{c}{b+c}\right)\)
\(=\dfrac{1}{2}.3=\dfrac{3}{2}\)