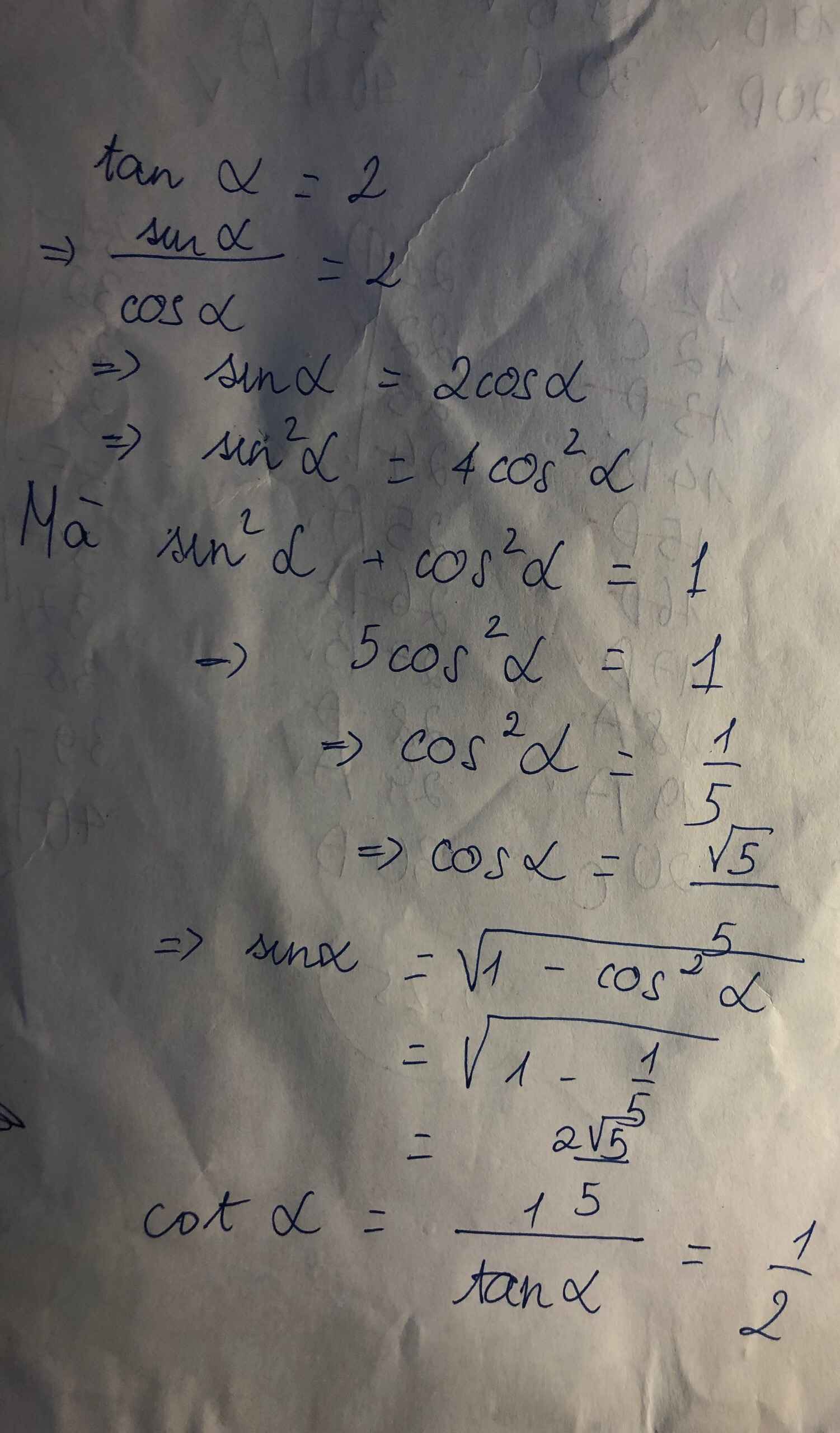Cho biết sinα = \(\frac{4}{5}\) . Tính cosα ; tanα ; cotα

\(\frac{4}{5}\) . Tính cosα ; tanα ; cotα

">

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

GV

Giang Vu Huong

26 tháng 8 2019

Cho biết sinα = \(\frac{4}{5}\) . Tính cosα ; tanα ; cotα

#Hỏi cộng đồng OLM #Toán lớp 9

1

TT

Trần Thị Như Ý

26 tháng 8 2019

https://i.imgur.com/DS9QNEp.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

GV

Giang Vu Huong

26 tháng 8 2019 - olm

Cho biết sinα = 4545 . Tính cosα ; tanα ; cotα

#Hỏi cộng đồng OLM #Toán lớp 9

3

NE

$๖ۣۜN๖ۣۜE๖ۣۜV ๖ۣۜE ๖ۣۜR $ ^^๖ۣۜG๖ۣۜ...

26 tháng 8 2019

dung may tinh la xong thui ban oi

hoac dua len mang giai

chao <>?

GV

Giang Vu Huong

26 tháng 8 2019

sinα = \(\frac{4}{5}\)

PT

Pham Trong Bach

28 tháng 9 2018

Cho A B C ^ = 60 0 và ∆ABC tam giác nhọna, Tính sinα, tanα, cotα, biết cosα = 1 5 b, Tính cosα, tanα, cotα, biết sinα = 2 3 c, Cho tanα = 2. Tính sinα, cosα, cotαd, Cho...

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

28 tháng 9 2018

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24

b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2

c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2

d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

KH

khanh hoa

24 tháng 8 2023

cho tanα = \(\dfrac{3}{4}\)tính sinα, cosα,...

#Hỏi cộng đồng OLM #Toán lớp 9

2

H9

HT.Phong (9A5)

CTVHS

24 tháng 8 2023

Ta có:

\(cot\alpha\cdot tan\alpha=1\)

\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}\)

\(\Rightarrow cota=\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)

Mà:

\(cot^2\alpha+1=\dfrac{1}{sin^2\alpha}\)

\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{cot^2\alpha+1}}\)

\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{\left(\dfrac{4}{3}\right)^2+1}}=\dfrac{3}{5}\)

Lại có:

\(cos^2\alpha+sin^2\alpha=1\)

\(\Rightarrow cos\alpha=\sqrt{1-sin^2a}\)

\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)

GH

Gia Huy

24 tháng 8 2023

\(tan\alpha=\dfrac{3}{4}\\ \Rightarrow cot\alpha=1:\dfrac{3}{4}=\dfrac{4}{3}\)

Có:

\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\\ \Rightarrow sin\alpha=\sqrt{1:\left(1+\left(\dfrac{4}{3}\right)^2\right)}=\dfrac{3}{5}\)

\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)

MH

myra hazel

21 tháng 10 2021

a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.

b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

21 tháng 10 2021

a: \(\cos\alpha=\dfrac{1}{2}\)

\(\tan\alpha=\sqrt{3}\)

\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)

KA

Khánh An Ngô

26 tháng 7 2023

tìm sinα cotα tanα biết cosα=\(\dfrac{1}{5}\)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

26 tháng 7 2023

\(1+tan^2a=\dfrac{1}{cos^2a}=1:\dfrac{1}{25}=25\)

=>tan^2a=24

=>tana=2*căn 6

\(cota=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)

\(sina=\sqrt{1-\left(\dfrac{1}{5}\right)^2}=\dfrac{2\sqrt{6}}{5}\)

C

Cindy

7 tháng 8 2021

Biết sinα=\(\dfrac{\sqrt{3}}{2}\).Tính cosα,tanα,cotα?

#Hỏi cộng đồng OLM #Toán lớp 9

1

IT

ミ★ήɠọς τɾίếτ★彡

7 tháng 8 2021

ta có :\(\sin2=\dfrac{\sqrt{3}}{2}\Rightarrow2=60^0\)

\(\cos60^o=\dfrac{1}{2};\tan60^o=\sqrt{3};\cot60^o=\dfrac{1}{\sqrt{3}}\)

LV

Luyện Văn Thịnh

27 tháng 8 2021 - olm

Bài 1: Cho biết cosα = 0,4. Hãy tìm sinα,tanα,cotα

#Hỏi cộng đồng OLM #Toán lớp 9

1

NM

Ngọc Mai_NBK

27 tháng 8 2021

TL:

Ta có: sin²α+cos²α= 1

=> sin²α=1−(0,4)²

=> sinα≈0,9

Mặt khác: tanα=sinα/cosα=0,9/0,4= 9/4

Mà: tanα×cotα=1

⇒cotα=4/9

PT

Pham Trong Bach

21 tháng 2 2019

Tìm cosα, tanα, cotα. biết sinα = 1 5

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

21 tháng 2 2019

Tương tự câu 2

PT

Pham Trong Bach

3 tháng 11 2019

Tìm sinα, cotα, tanα biết cosα = 1 5

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

3 tháng 11 2019

Gợi ý: Sử dụng công thức: sin 2 α + cos 2 α = 1

JP

James Pham

4 tháng 8 2021

Bài 1: Biết sinα = \(\dfrac{\sqrt{3}}{2}\). Hãy tính cosα, tanα, cotα.
Bài 2: Biết tanα = 2. Hãy tính sinα, cotα, cosα
Bài 3: Tính: A= cos²20^o + cos²40^o + cos²50^o + cos²70^o

#Hỏi cộng đồng OLM #Toán lớp 9

2

👁💧👄💧👁

4 tháng 8 2021

Ảnh 1 là bài 1,3. Ảnh 2 là bài 2 nhé bạn.

undefined

undefined

NL

Nguyễn Lê Phước Thịnh

4 tháng 8 2021

Bài 3:

Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)

\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)

=1+1

=2