Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
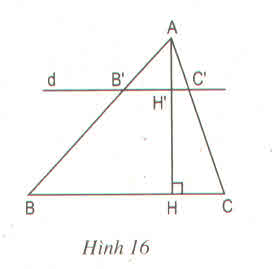
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2
Lời giải
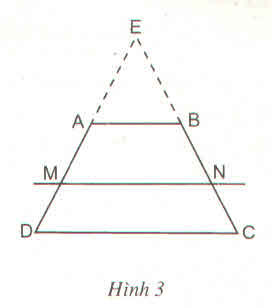
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???
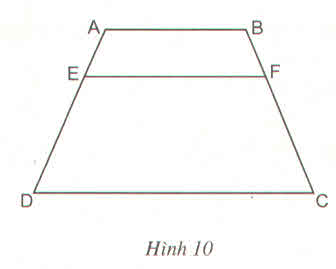
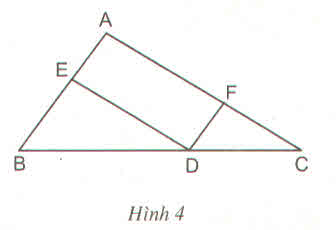
Trong ∆ ABC ta có: DE // AC (gt)
Suy ra: \(\frac{AE}{AB}=\frac{CD}{CB}\)(định lí Ta-lét) (1)
Lại có: DF // AB (gt)
Suy ra: \(\frac{AF}{AC}=\frac{BD}{BC}\)(định lí Ta-lét) (2)
Cộng trừ vế (1) và (2), ta có:
\(\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{BC}{BC}=1\)
DÚP MK VS NHÉ! 
MK CẦN GẮP LÉM Ạ!
THANKS MẤY BN DÚP MK NHỀU NHỀU NHÂN!
a) Ta có:
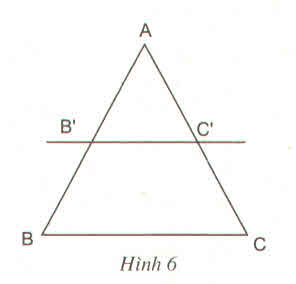
AB′ABAB′AB = AC′ACAC′AC => ACAC′ACAC′ = ABAB′ABAB′
=> ACAC′ACAC′ - 1 = AC−AC′AC′AC−AC′AC′ = AB−AB′AB′AB−AB′AB′
=> CC′AC′CC′AC′ = B′BAB′B′BAB′ => AB′BB′AB′BB′ = AC′CC′AC′CC′
b) Vì AB′ABAB′AB = AC′ACAC′AC mà AB' = AB - B'B, AC' = AC - C'C.
a) Ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\Rightarrow\dfrac{AB}{AC}=\dfrac{AB'}{AC'}\)
Áp dụng tc dãy tỉ số bằng nhau ta có;
\(\dfrac{AB}{AC}=\dfrac{AB'}{AC'}=\dfrac{AB-AB'}{AC-AC'}=\dfrac{BB'}{CC'}\)
\(\Rightarrow\dfrac{AB'}{AC'}=\dfrac{BB'}{CC'}\Leftrightarrow\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)
b) Ta có:
\(\dfrac{AB}{AC}=\dfrac{BB'}{CC'}\left(cmt\right)\)
\(\Leftrightarrow\dfrac{AB}{BB'}=\dfrac{AC}{CC'}\Leftrightarrow\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)