Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(t=3^x,t>0\)
Bất phương trình trở thành :
\(m.t^2+9\left(m-1\right)t+m-1>0\)
\(\Leftrightarrow m\left(t^2+9t+1\right)>9t+1\)
\(\Leftrightarrow m>\frac{9t+1}{t^2+9t+1}\)
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi :
\(m>max_{t>0}\frac{9t+1}{t^2+9t+1}\)
Xét hàm số \(f\left(t\right)=\frac{9t+1}{t^2+9t+1};t>0\)
Ta có : \(f'\left(t\right)=\frac{-9t-2}{\left(t^2+9t+1\right)^2}< 0,t>0\)
đây là hàm nghịch biến suy ra \(f\left(t\right)< f\left(0\right)=1\)
Do đó : \(\frac{9t+1}{t^2+9t+1}< 0,t>0\) nên các giá trị cần tìm là \(m\ge1\)

Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)

a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0

bpt (1) \(\Leftrightarrow x\in\left(-5;3\right)\)=> S1=(-5;3)
bpt (2):
Nếu m=-1 =>S2=\(\varnothing\)
Nếu m>-1 =>S2=\(\left[\frac{3}{m+1};+\infty\right]\)
Nếu m<-1 => S2=\(\left[-\infty;\frac{3}{m+1}\right]\)
Hệ có nghiệm \(\Leftrightarrow S1\cap S2\ne\varnothing\)
Nếu m=-1 =>\(S1\cap S2=\varnothing\) (Loại)
Nếu m>-1 =>\(S1\cap S2\ne\varnothing\)
Nếu m<-1 =>\(S1\cap S2\ne\varnothing\)
vì sao mà hệ có nghiệm thì S1 giao S2 phải khác tập hợp rỗng ? mà tại sao bạn lại biện luận bất phương trình như vậy ?

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
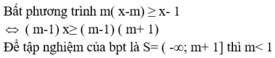
Chọn C.
Ta có: m(x - m) ≤ x - 1 ⇔ mx - m 2 ≥ x - 1 ⇔ (m - 1)x ≥ m 2 - 1
+) Với m < 1 ⇒ m – 1 < 0 ⇒ Tập nghiệm của bất phương trình là S = ( - ∞ ;m+1].
+) Với m > 1 ⇒ m – 1 > 0 ⇒ Tập nghiệm của bất phương trình là S = [m+1; + ∞ ).