Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
Do a, b, c là ba số liên tiếp của một cấp số cộng có công sai là 2
nên b = a + 2, c = a + 4
a + 1, a + 3, a + 7 là ba số liên tiếp của một cấp số nhân
⇔ a + 1 a + 7 = a + 3 2
⇔ a = 1
Với a = 1 ta có b = 3 c = 5
Suy ra a + b + c = 9

a) Có \(u_n=\left(-3\right)^{2n-1}=\left(-3\right)^2.\left(-3\right)^{2n-3}\)\(=9.2^{2\left(n-1\right)-1}=9.u_{n-1}\)
Vì vậy \(\left(u_n\right)\) là dãy số nhân với \(u_1=\left(-3\right)^{2.1-1}=-3\) và \(q=9\).
b) Công thức truy hồi của dãy số \(\left(u_n\right)\) là \(u_n=9u_{n-1}\).
c) Có \(u_n=\left(-3\right)^{2n-1}=-19683=\left(-3\right)^9\)\(\Leftrightarrow2n-1=9\)\(\Leftrightarrow n=5\).
Vậy số hạng thứ 5 bằng \(-19683\).

Theo giả thiết, nếu ba dố a, b, c lập thành cấp số nhân thì : \(ac=b^2\)(1)
Lấy Logarit cơ số N hai vế của (1) ta có :
\(\Leftrightarrow\log_N\left(ac\right)=\log_Nb^2\Leftrightarrow\log_Na+\log_Nc=2\log_Nb\left(2\right)\)
Sử dụng công thức đổi cơ số :
Từ (2) \(\Leftrightarrow\frac{1}{\log_aN}+\frac{1}{\log_cN}=\frac{2}{\log_bN}\Leftrightarrow\frac{1}{\log_aN}-\frac{1}{\log_bN}=\frac{1}{\log_bN}-\frac{1}{\log_cN}\)
\(\Leftrightarrow\frac{\log_bN-\log_aN}{\frac{1}{\log_aN}.\frac{1}{\log_bN}}=\frac{\log_cN-\log_bN}{\frac{1}{\log_cN}.\frac{1}{\log_bN}}\Leftrightarrow\frac{\log_bN-\log_aN}{\frac{1}{\log_cN}-\frac{1}{\log_bN}}=\frac{\log_aN}{\log_cN}\)
\(\Rightarrow\frac{\log_aN-\log_bN}{\frac{1}{\log_bcN}-\frac{1}{\log_cN}}=\frac{\log_aN}{\frac{1}{\log_cN}}\)

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
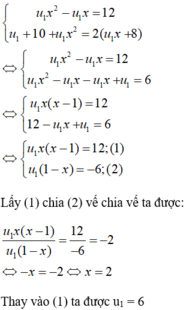
+ Tổng của năm số hạng đầu của CSN là:


Gọi 3 số đó là: \(a,b,c\). Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b+c=114\\b^2=ac\end{matrix}\right.\). (*)
Mặt khác nó lần lượt là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng nên: \(a=u_1;b=u_1+3d;c=u_1+24d\). ( với \(u_1\) là số hạng đầu của cấp số cộng, d là công sai).
Thay vào (*) ta có:
\(\left\{{}\begin{matrix}u_1+u_1+3d+u_1+24d=114\\\left(u_1+3d\right)^2=u_1\left(u_1+24d\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\18u_1d-9d^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\9d\left(2u_1-d\right)=0\end{matrix}\right.\).
Nếu \(d=0\) thì a,b,c là ba số hạng của một cấp số cộng không đổi nên \(a=b=c=\sqrt[3]{114}\).
Nếu \(d\ne0\) suy ra: \(\left\{{}\begin{matrix}u_1+9d=38\\2u_1-d=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=2\\d=4\end{matrix}\right.\).
Khi đó \(a=2;b=2+3.4=16;c=2+24.3=74\).
