Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

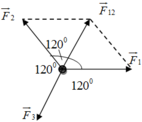
Theo bài ra ( F 1 → ; F → 2 ) = 120 0 ; F 1 = F 2 nên theo quy tắc tổng hợp hình bình hành và tính chất hình thoi
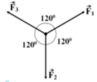
Ta có ( F 1 → ; F → 12 ) = 60 0 ; F 1 = F 2 = F 12 = 80 N
Mà ( F 12 → ; F → 3 ) = 180 0 ⇒ F → 12 ↑ ↓ F → 3
Vậy F = F 12 − F 3 = 80 − 80 = 0 N

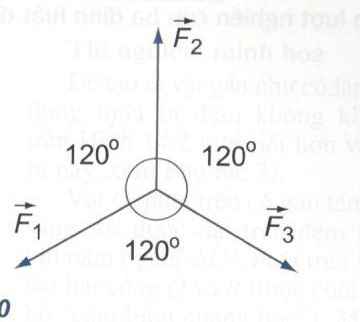
Biểu diễn thành hình sau:
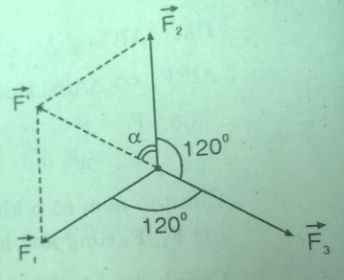
HBH \(OF_1F'F_2\) gồm hai tam giác đều:
\(\Rightarrow F'=F_1=F_2=F_3\) và \(\alpha=60^o\)
Có \(F'vàF_3\) là hai vecto ngược chiều
\(\Rightarrow\overrightarrow{F}=\overrightarrow{F'}+\overrightarrow{F_3}=\overrightarrow{0}\)

Chọn A.
Do tính đối xứng nên tổng hợp ba véc tơ bằng véc tơ không.

Chọn A.
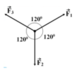
Do tính đối xứng nên tổng hợp ba véc tơ bằng véc tơ không.

Ta có :
Trọng lực của thanh đặt ở trung điểm thanh (gọi G là trung điểm thanh AB)
Ta giải bài toán trong trường hợp tổng,
Áp dụng quy tắc momen trục quay tại B:
\(mg.BGsin\alpha=F.BA\)
\(\rightarrow F=mg\frac{BGsin\alpha}{BA}=50.10\frac{sin\alpha}{2}=250sin\alpha\)
Phản lực của tường phải cân bằng với F và P.
Phản lực theo phương ngang: \(N_x=F.sin\alpha\)
Phản lực theo phương thẳng đứng:\(N_y=mg-F.cos\alpha\)
Gọi góc hợp giữa phản lực và phương ngang là \(\phi\)
\(tan\phi=\frac{Ny}{Nx}=\frac{mg-Fcos\alpha}{Fsin\alpha}\)
\(=\frac{500-250sin\alpha.cosalpha}{250sinalpha^2}=\frac{2-sin\alpha.cosalpha}{sinalpha^2}\)
Độ lớn của phản lực:
\(N=\sqrt{N_x^2+N^2_y}=\sqrt{F^2+m^2g^2-2mgFcosalpha}\)
Trong 2 trường hợp góc α này chúng ta thay số và tìm các giá trị cần tìm
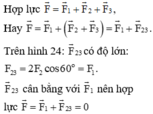

Chọn đáp án D
? Lời giải: