

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn C.
Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Đáp án D
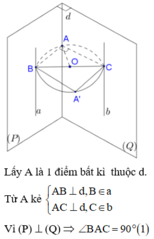
Ta đi chứng minh BC chính là khoảng cách giữa hai đường thẳng a và b, BC = 4:
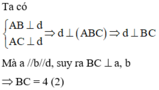
Từ (1) (2) suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2

AD // CF ---> AFCD là hbh ---> AF = CD
DK // BC ---> DKBC là hbh ---> BK = CD
---> AB-AF = AB-BK hay FB = AK (1)
AM // FB ---> ^MAK = ^PFB (góc đồng vị) (2)
MK // PB ---> ^MKA = ^PBF (góc đồng vị) (3)
(1),(2),(3) ---> 2 t/g MAK và PFB bằng nhau (gcg) ---> MA = PF (4)
Mà AC // PF ---> MA // PF (5)
(4),(5) ---> MAFB là hbh ---> MP // AF ---> MP // AB
b)
Gọi Q là giao điểm của MP và CF, B' là giao điểm của DQ và AB ---> B và B' nằm cùng phía đối với đt CF
CD // FB' ---> 2 t/g QCD và QFB' đồng dạng ---> QC/QF = CD/FB' (5)
QP // FB ---> QC/QF = PC/PB (6)
FB // AC ---> PC/PB = FA/FB = CD/FB (7)
(5),(6),(7) ---> FB' = FB
Mà B và B' nằm cùng phía đối với đt CF nên B' trùng B ---> DB đi qua Q hay nói cách khác MP,CF,DB đồng quy tại Q