Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề,ta có:
Góc AOB= góc A'OB'( 2 góc đối đỉnh)
Góc AOx= góc A'Ox'(2 góc đối đỉnh).
Góc BOx= góc B'Ox'(2 góc đối đỉnh).
Mà góc AOx=góc BOx( vì tia Ox là tia phân giác của góc AOB).
=> Góc A'Ox'= góc B'Ox'. /1/
Vì Ox là tia phân giác của góc AOB.
=> Tia Ox nằm giữa 2 tia OA,OB. /2/
Ta lại có góc AOB và góc A'OB' là 2 góc đối đỉnh, tia Ox' là tia đối của tia Ox. /3/
Từ /2/ và /3/ => Tia Ox' nằm giữa 2 tia OA' và OB'. /4/
Từ /1/ và /4/ => Tia Ox' là tia phân giác của góc A'OB'( đpcm)

a: \(\widehat{AOB}=160^0\cdot\dfrac{7}{8}=140^0\)
\(\widehat{BOC}=160^0-140^0=20^0\)
b: \(\widehat{AOD}=160^0-90^0=70^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOD}< \widehat{AOB}\)
nên tia OD nằm giữa hai tia OA và OB
mà \(\widehat{AOD}=\dfrac{1}{2}\widehat{AOB}\)
nên OD là tia phân giác của góc AOB

Đề bài có vấn đề gì không nhỉ?
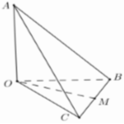
Tam giác OAB vuông cân tại O nên OM là trung tuyến đồng thời là đường cao
\(\Rightarrow OM\perp AB\) hay góc giữa OM và AB bằng 90 độ (cosin góc giữa 2 đường thẳng bằng 0)

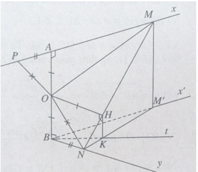
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
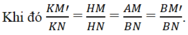
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

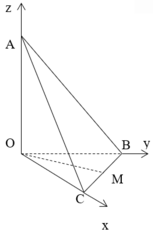
Tam giác OAB vuông cân tại O
\(\Rightarrow OM\perp AB\)
\(\Rightarrow\) cosin góc giữa 2 đường thẳng này bằng 0