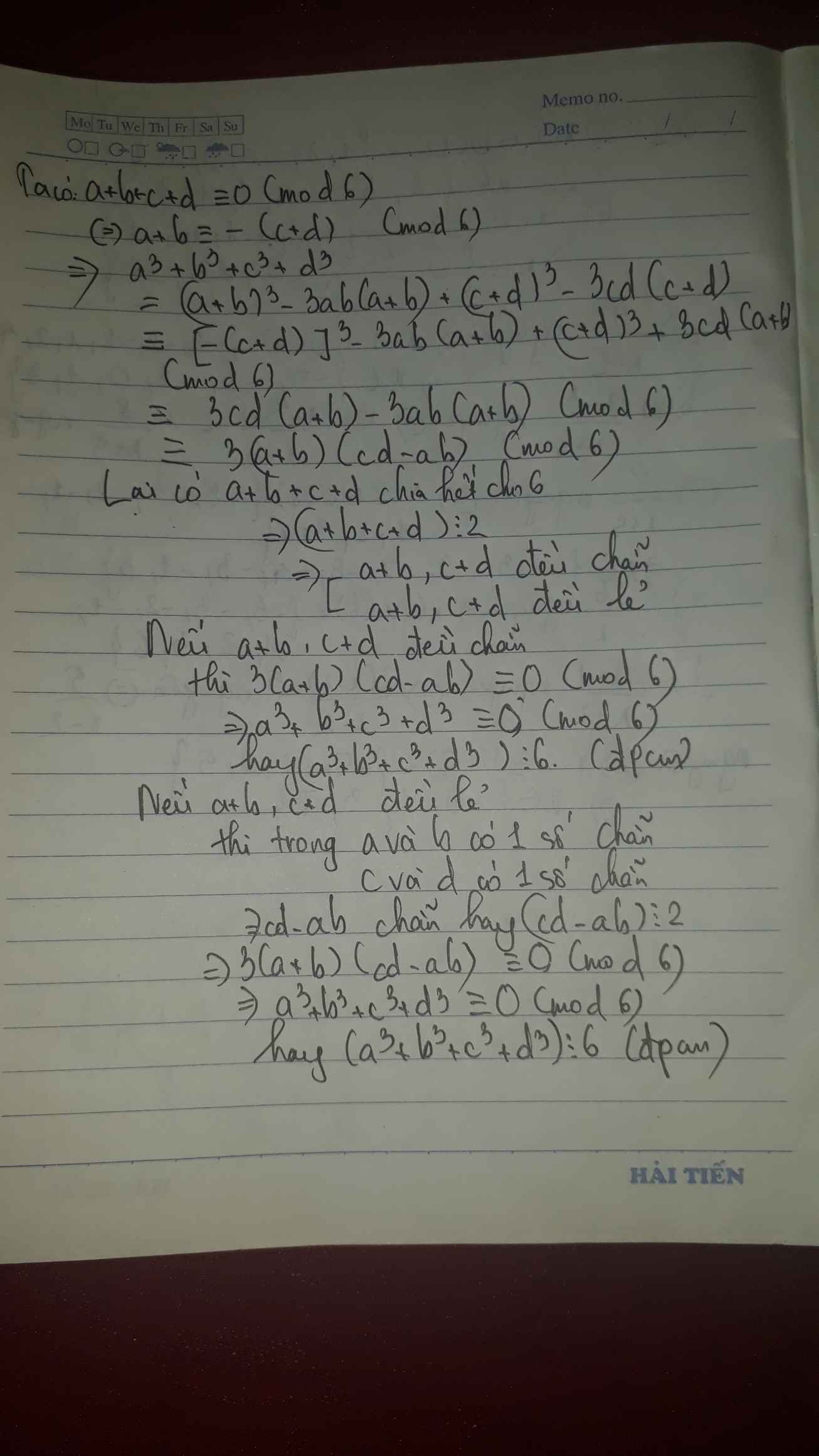LQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PL
1
17 tháng 7 2016
Ta có :(a+b+c)3=a3+b3+c3+3a2b+3a2c+3b2c+3b2a+3c2a+3c2b+6abc
(a+b+c)3=a3+b3+c3+(3a2b+3a2b+3abc)+(3b2c+3b2a+3abc)+(3c2a+3c2b+3abc)-3abc
(a+b+c)3=a3+b3+c3+3ab(a+b+c)+3bc(a+b+c)+3ac(a+b+c)-3abc
(a+b+c)3=a3+b3+c3+3(a+b+c)(ab+bc+ac)-3abc
thay a+b+c=0 ta được
03=a3+b3+c3+3.0(ab+bc+ac)-3abc
0=a3+b3+c3-3abc
=>a3+b3+c3=3abc
15 tháng 7 2019
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{d}{5}\) và a+b+c+d=-42
Áp dụng tính chất dãy tỉ số bằng nhau, ta có;
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{d}{5}=\frac{a+b+c+d}{2+3+4+5}=\frac{-42}{14}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{a}{2}=-3\Rightarrow a=-6\\\frac{b}{3}=-3\Rightarrow b=-9\\\frac{c}{4}=-3\Rightarrow c=-12\\\frac{d}{5}=-3\Rightarrow d=-15\end{matrix}\right.\)
+)
28 tháng 5 2022
Bài 8:
a: \(\left(\dfrac{2}{5}+\dfrac{3}{4}\right)^2=\left(\dfrac{8+15}{20}\right)^2=\left(\dfrac{23}{20}\right)^2=\dfrac{529}{400}\)
b: \(\left(\dfrac{5}{4}-\dfrac{1}{6}\right)^2=\left(\dfrac{15}{12}-\dfrac{2}{12}\right)^2=\left(\dfrac{13}{12}\right)^2=\dfrac{169}{144}\)
28 tháng 7 2021
Bài này cần dùng một ít kiến thức của lớp 8, bạn có thể tìm hiểu thêm.
