Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài sai, M là trung điểm của BC thì sao AM vuông góc với BC? cà thái thành

a) Xét ΔABM và ΔCKM có:
MA=MC(gt)
MB=MK(gt)
góc BMA= góc CMK( 2 góc đối đỉnh )
=>ΔABM=ΔCKM( c.g.c)
=> góc MAB= góc MCK=90o
=>KC vuông góc với AC
b) Xét ΔBMC và ΔKMA có:
MA=MC(gt)
góc BMC= góc AMK( 2 góc đối đỉnh )
=>ΔBMC=ΔKMA(c.g.c)
=> góc MBC= góc MKA
=>BC//AK
a) Ta có: A1ˆ+A2ˆ+A3ˆ=180o( góc bẹt )
⇒A1ˆ+A3ˆ=90o( do A2ˆ=90o ) (1)
Trong ΔAKC có: A3ˆ+C1ˆ=90o( do Kˆ=90o) (2)
Từ (1) và (2) ⇒A1ˆ=C1ˆ
Xét ΔAHB,ΔCKA có:
A1ˆ=C1ˆ(cmt)
AB = AC ( gt )
H^=K^=90o
⇒ΔAHB=ΔCKA( c.huyền - g.nhọn )
⇒AH=CK( cạnh t/ứng ) ( đpcm )
b) Vì ΔAHB=ΔCKA
⇒BH=AK,AH=CK( cạnh t/ứng )
Ta có: HK=AK+AH=BH+CK(đpcm)
Vậy...
Chúc bạn học tốt

Câu a
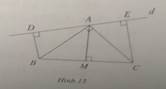
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
a) Xét hai tam giác vuông:\(\Delta AMB\) và \(\Delta AMC\) có:
\(BM=MC\left(gt\right)\)
AM là cạnh chung
\(\Rightarrow\Delta AMB=\Delta AMC\) (hai cạnh góc vuông)
\(\Rightarrow AB=AC\) (hai cạnh tương ứng)
b) Vẽ tia đối của tia AB là tia Ay
Ta có:
\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow AC\perp Ay\)
\(\Rightarrow\widehat{yAK}+\widehat{KAC}=90^0\)
Lại có:
\(\widehat{yAK}=\widehat{BAH}\) (đối đỉnh)
\(\Rightarrow\widehat{BAH}+\widehat{KAC}=90^0\)
Mà \(\widehat{ACK}+\widehat{KAC}=90^0\) (\(\Delta ACK\) vuông tại K)
\(\Rightarrow\widehat{BAH}=\widehat{ACK}\)
Do \(\Delta AMB=\Delta AMC\left(cmt\right)\)
\(\Rightarrow AB=AC\) (hai cạnh tương ứng)
Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CKA\) có:
\(AB=AC\left(cmt\right)\)
\(\widehat{BAH}=\widehat{ACK}\left(cmt\right)\)
\(\Rightarrow\Delta AHB=\Delta CKA\) (cạnh huyền - góc nhọn)