Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
c: \(AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\)



Câu 2:
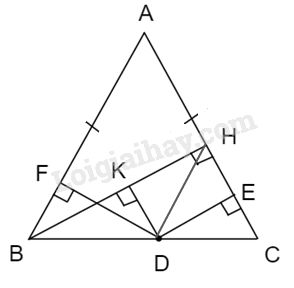
Kẻ \(DK\perp BH.\)
Mà \(BH\perp AC\left(gt\right)\)
=> \(DK\) // \(AC\) (từ vuông góc đến song song).
Hay \(DK\) // \(HC.\)
=> \(\widehat{KDB}=\widehat{HCD}\) (vì 2 góc đồng vị).
+ Vì \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{HCD}.\)
Mà \(\widehat{KDB}=\widehat{HCD}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{KDB}.\)
Xét 2 \(\Delta\) vuông \(BFD\) và \(DKB\) có:
\(\widehat{BFD}=\widehat{DKB}=90^0\)
Cạnh BD chung
\(\widehat{FBD}=\widehat{KDB}\left(cmt\right)\)
=> \(\Delta BFD=\Delta DKB\) (cạnh huyền - góc nhọn).
=> \(DF=BK\) (2 cạnh tương ứng) (1).
Nối D với H.
+ Vì \(DK\) // \(AC\left(cmt\right)\)
=> \(DK\) // \(EH.\)
=> \(\widehat{KDH}=\widehat{EHD}\) (vì 2 góc so le trong).
Xét 2 \(\Delta\) vuông \(DEH\) và \(HKD\) có:
\(\widehat{DEH}=\widehat{HKD}=90^0\)
Cạnh DH chung
\(\widehat{EHD}=\widehat{KDH}\left(cmt\right)\)
=> \(\Delta DEH=\Delta HKD\) (cạnh huyền - góc nhọn).
=> \(DE=HK\) (2 cạnh tương ứng) (2).
Từ (1) và (2) => \(DF+DE=BK+HK.\)
Mà \(BK+HK=BH\)
=> \(DF+DE=BH\left(đpcm\right).\)
Chúc bạn học tốt!