Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét ΔHBA và ΔABC:
\(\widehat{H}=\widehat{A}=90^0\left(gt\right)\)
\(\widehat{B}chung\)
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A:
Theo đ/lí Py - ta - go ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=12^2+16^2\)
\(BC^2=400\)
\(\Rightarrow BC=\sqrt{400}=20cm\)
Ta có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Rightarrow\dfrac{AH}{16}=\dfrac{12}{20}\)
\(\Rightarrow AH=9,6cm\)
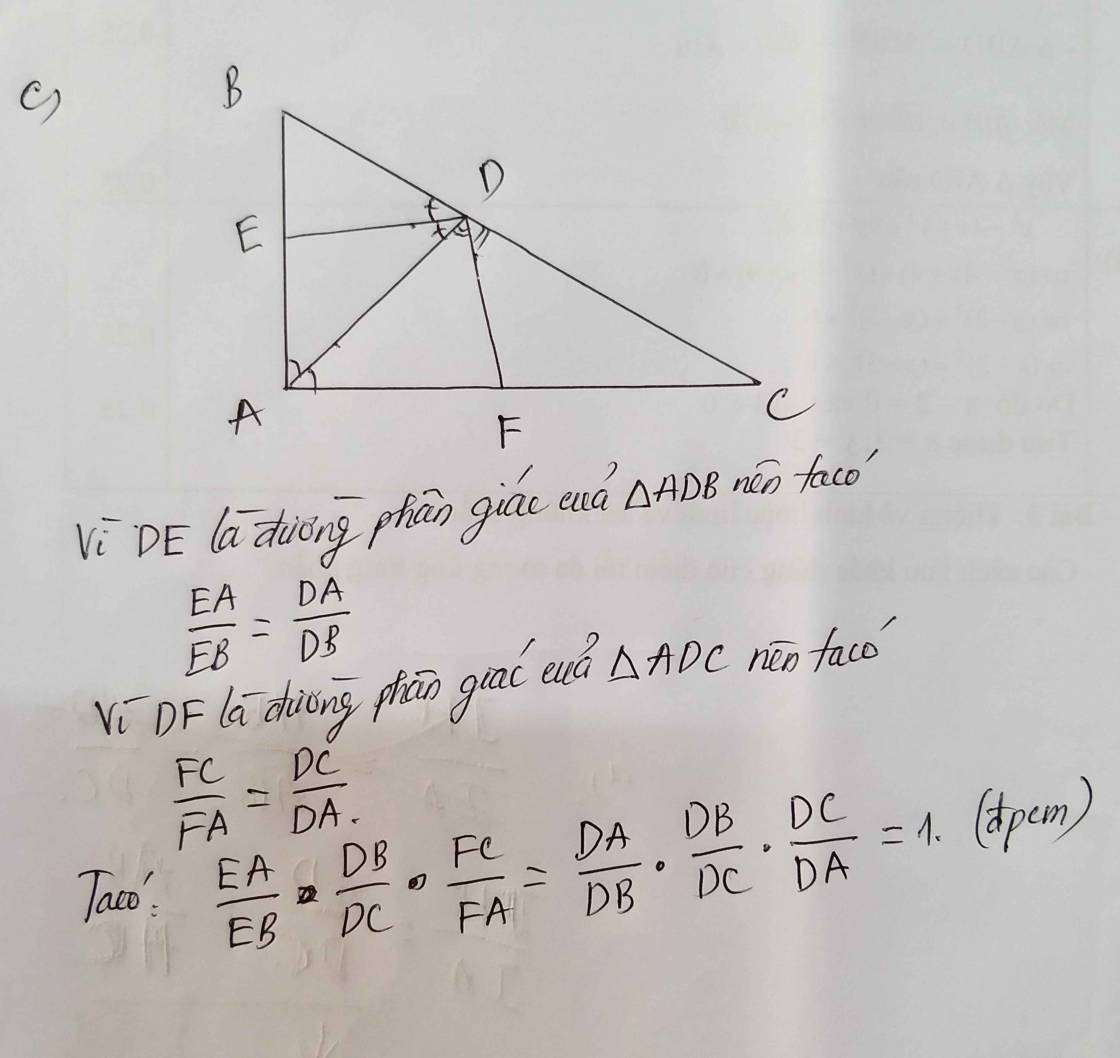
c. Ta có DE là đường phân giác \(\widehat{ADB}\)
\(\rightarrow\dfrac{EA}{EB}=\dfrac{DA}{DB}\left(1\right)\)
DF là đường phân giác \(\widehat{ADC}\)
\(\rightarrow\dfrac{FC}{FA}=\dfrac{DC}{DA}\left(2\right)\)
AD là đường phân giác \(\widehat{ABC}\)
\(\rightarrow\dfrac{DC}{DB}=\dfrac{AC}{AB}\left(3\right)\)
Từ (1) và (2),(3) \(\Rightarrow\) \(\dfrac{EA}{EB}.\dfrac{FC}{FA}.\dfrac{DB}{DC}=\dfrac{DA}{DB}.\dfrac{DC}{DA}.\dfrac{AC}{AB}\)
\(\Rightarrow\dfrac{EA}{EB}.\dfrac{FC}{FA}.\dfrac{DC}{DB}=\dfrac{DB}{DC}.\dfrac{AC}{AB}=\dfrac{AB}{AC}.\dfrac{AC}{AB}=1\)
Vậy ...
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b:BC=căn 12^2+16^2=20cm
AH=12*16/20=9,6cm

a)
Xét \(\Delta\)HBA và \(\Delta\)HAC
có: ^BHA = ^AHC = 90 độ
^HBA = ^HAC ( cùng phụ ^HAB )
=> \(\Delta\)HBA ~ \(\Delta\)HAC
b) Ta có: \(BC=\sqrt{AB^2+AC^2}=10\)cm
=> \(S\left(ABC\right)=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)
=> \(AH=\frac{6.8}{10}=4,8\)cm
c) Tích chất phân giác
=> \(\frac{AB}{BC}=\frac{AD}{DC}\Rightarrow\frac{AD}{6}=\frac{DC}{10}=\frac{AD+DC}{6+10}=\frac{8}{16}=\frac{1}{2}\)
=> AD = 3 cm; DC = 5 cm
Theo pi ta go trong \(\Delta\)ADB => \(BD=\sqrt{AB^2+AD^2}=\sqrt{6^2+3^2}=3\sqrt{5}\)
A B C D H
a) \(\Delta ABC\)vuông tại A \(\Rightarrow\widehat{ABC}+\widehat{C}=90^o\)
\(\Delta AHC\)vuông tại H \(\Rightarrow\widehat{HAC}+\widehat{C}=90^o\)
\(\Rightarrow\widehat{HAC}=\widehat{ABC}\)
Xét \(\Delta HBA\)và \(\Delta HAC\)có:+) \(\widehat{AHB}=\widehat{AHC}=90^o\)
+) \(\widehat{HAC}=\widehat{ABC}\)
\(\Rightarrow\Delta HBA~\Delta HAC\left(g-g\right)\)( đpcm )
b) \(\Delta ABC\)vuông tại A \(\Rightarrow AB^2+AC^2=BC^2\)( định lý Pytago )
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
Xét \(\Delta ABC\)có: \(S=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)
\(\Rightarrow AB.AC=AH.BC\)\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)
c) \(\Delta ABC\)có BD là phân giác \(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{6}{10}=\frac{3}{5}\)
\(\Rightarrow\frac{AD}{3}=\frac{DC}{5}=\frac{AD+DC}{3+5}=\frac{AC}{8}=\frac{8}{8}=1\)
\(\Rightarrow DC=5.1=5\); \(AD=3.1=3\)
Xét \(\Delta ABD\)vuông tại A \(\Rightarrow AB^2+AD^2=BD^2\)( định lý Pytago )
\(\Rightarrow BD=\sqrt{AB^2+AD^2}=\sqrt{6^2+3^2}=\sqrt{54}=3\sqrt{6}\)

Hình bạn tự vẽ nhé...
a)
Xét tam giác BAH và tam giác ABC , có :
A^ = H^ = 90O
B^ : góc chung
=> tam giác HAB ~ tam giác ACB ( g.g)
c)
ADĐL pitago vào tam giác vuông ABC , có :
AB2 + AC2 = BC2
=> 122 + 166 = BC2
=> BC2 = 400
=> BC = 20 cm
Vì tam giác ACB ~ tam giác HAB , nên ta có :
AH/AC= AB/BC
=> AH/16=12/20
=> AH = 9,6 cm.

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6

Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = \sqrt{400}400= 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=> \frac{AH}{AC}=\frac{AB}{BC}hay\frac{AH}{16}=\frac{12}{20}ACAH=BCABhay16AH=2012
=> AH = \frac{12.16}{20}=9,62012.16=9,6( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = \sqrt{51,84}51,84 = 7,2 ( cm )
c) Vì AD là đường phân giác của tam giác ABC nên :
\frac{AB}{BD}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BC-CD}=\frac{AC}{CD}BDAB=CDAC⇔BC−CDAB=CDAC
<=> \frac{AB.CD}{CD\left(BC-CD\right)}=\frac{AC\left(BC-CD\right)}{CD\left(BC-CD\right)}CD(BC−CD)AB.CD=CD(BC−CD)AC(BC−CD)
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD = \frac{320}{28}\approx11.43\left(cm\right)28320≈11.43(cm)
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - \frac{320}{28}28320\approx≈ 8,57 ( cm )

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6