Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình cx ko bik nx tại vì này là thầy mình chụp bài của bên trường gửi qua lớp mình á, này là thầy mình gửi qua á

a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 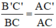
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 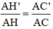
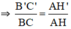
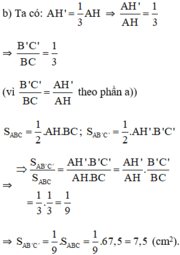

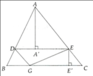
Xét ΔCAB có KD//AB
nên ΔCDK đồng dạng với ΔCBA
=>\(\dfrac{S_{CDK}}{S_{CBA}}=\left(\dfrac{CD}{CB}\right)^2\)
=>\(S_{CBA}=16:\dfrac{CD^2}{CB^2}=16\cdot\dfrac{CB^2}{CD^2}\)
Xét ΔBED và ΔBAC có
góc BED=góc BAC
góc B chung
=>ΔBED đồng dạng với ΔBAC
=>\(\dfrac{S_{BED}}{S_{BAC}}=\left(\dfrac{BD}{BC}\right)^2\)
=>\(S_{ABC}=9\cdot\dfrac{BC^2}{BD^2}=16\cdot\dfrac{BC^2}{CD^2}\)
=>3/BD=4/CD
=>BC=7/3BD
=>\(\dfrac{S_{BED}}{S_{BAC}}=\left(\dfrac{3}{7}\right)^2=\dfrac{9}{49}\)
=>\(S_{BAC}=49\left(cm^2\right)\)
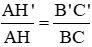 .
.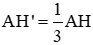 và diện tích tam giác ABC là 67,5 cm
và diện tích tam giác ABC là 67,5 cm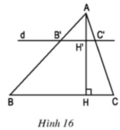
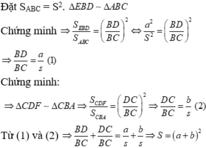
A C B M N P S1 S2 S3
Đặt BM=b, MC=a và diện tích tam giác ABC là S
do b<a nên S1<S2 nên S1=6.25
Ta có: \(\frac{S_1}{S}=\left(\frac{a}{a+b}\right)^2\)
\(\frac{S_2}{S}=\left(\frac{b}{a+b}\right)^2\)
=>\(\frac{S_1}{S_2}=\frac{a^2}{b^2}=\frac{6.25}{12.4609}\)
<=> \(\frac{a}{b}=\frac{2.5}{3.53}\)<=>\(\frac{a}{a+b}=\frac{2.5}{2.5+3.53}=\frac{2.5}{6.03}\)Thay vào S1/S
S1= 6,25=> S=15.075