Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
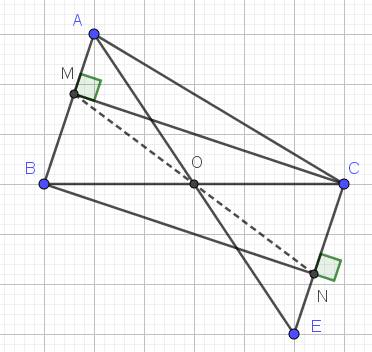
a. Xét tam giác $AOB$ và $EOC$ có:
$\widehat{AOB}=\widehat{EOC}$ (đối đỉnh)
$AO=EO$ (gt)
$OB=OC$ (do $O$ là trung điểm $BC$)
$\Rightarrow \triangle AOB=\triangle EOC$ (c.g.c)
b.
Từ tam giác bằng nhau phần a suy ra:
$AB=EC$ (đpcm)
$\widehat{OAB}=\widehat{OEC}$. Mà 2 góc này ở vị trí so le trong nên $AB\parallel CE$ (đpcm)
c.
Xét tam giác $BMC$ và $CNB$ có:
$\widehat{BMC}=\widehat{CNB}=90^0$
$BC$ chung
$\widehat{MBC}=\widehat{NCB}$ (so le trong)
$\Rightarrow \triangle BMC=\triangle CNB$ (g.c.g)
$\Rightarrow BM=NC$
Xét tam giác $BMO$ và $CNO$ có:
$BM=CN$ (cmt)
$\widehat{MBO}=\widehat{NCO}$ (so le trong)
$BO=CO$
$\Rightarrow \triangle BMO=\triangle CNO$ (c.g.c)
$\Rightarrow \widehat{BOM}=\widehat{CON}$
$\Rightarrow \widehat{BOM}+\widehat{BON}=\widehat{CON}+\widehat{BON}$
$\Rightarrow \widehat{MON}=\widehat{BOC}=180^0$
$\Rightarrow M, O, N$ thẳng hàng.

a: Ta có: ΔBDC vuông tại D
mà DO là đường trung tuyến
nên DO=BC/2

a. Xét tam giac ABM và tam giac ACM có
AB=AC(gt)
góc B=góc C(tam giac ABC cân)
AM cạnh chung
suy ra tam giac ABM=tam giac ACM
b. ta có:
tam giác ABC cân mà AM là đường trung tuyến nên AM cũng là đường cao
suy ra AM vuông goc vs BC

A B C M N F E
a) Xét \(\Delta BNM\)và \(\Delta ACM\)có :
NM = MC ( gt )
\(\widehat{NMB}=\widehat{CMA}\)( hai góc đối đỉnh )
MB = MA ( gt )
Suy ra : \(\Delta BNM\)= \(\Delta ACM\)( c.g.c )
\(\Rightarrow NB=AC\)( hai cạnh tương ứng )
\(\Rightarrow\widehat{BNM}=\widehat{ACM}\)( hai góc tương ứng )
Mà hai góc này ở vị trí so le trong nên NB // AC
b) Xét \(\Delta BNC\)có \(\widehat{EBC}\)là góc ngoài nên \(\widehat{EBC}\)= \(\widehat{BNC}+\widehat{BCN}\)hay \(\widehat{EBC}\)= \(\widehat{ACM}+\widehat{BCN}=\widehat{ACB}\)
Xét \(\Delta BEC\)và \(\Delta BAC\)có :
BE = AC ( vì NB = BE = AC )
\(\widehat{EBC}\)= \(\widehat{ACB}\)( cmt )
BC ( cạnh chung )
Suy ra : \(\Delta BEC\)= \(\Delta BAC\)( c.g.c )
\(\Rightarrow AB=EC\)( hai cạnh tương ứng )
c) Vì \(\widehat{EFC}=\widehat{AFB}\)( hai góc đối đỉnh )
Mà \(\widehat{AFB}=180^o-\widehat{AFC}\)
\(\Rightarrow\widehat{EFC}+\widehat{AFC}=180^o-\widehat{AFC}+\widehat{AFC}=180^o\)
\(\Rightarrow\widehat{AFE}\)là góc bẹt nên A,F,E thẳng hàng

câu d vẽ tam giác đều ACO .từ o kẻ đường vuông góc với hk tại p.tam giác CAH BẰNG tam giác COP cạnh huyền góc nhọn. suy ra CP=AH SUY RA PK=PC=AH.tam giác OKP BẰNG tam giác OCP C.G.C SUY RA GÓC OKC = 15 . GÓC AKC=30 suy ra góc KAC = 180-30-75=75 SUY RA BAK=45

a) Xét ΔABF và ΔCNF có:
AF = CF (F là trung điểm của AC)
∠AFB = CFN (2 góc đối đỉnh)
FB = FN (gt)
⇒ ΔABF = ΔCNF (c.g.c)
⇒ ∠ABF = ∠CNF (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong ⇒ AB // NC
Xét ΔACE và ΔBME có:
AE = BE (E là trung điểm của AB)
∠AEC = ∠BEM (2 góc đối đỉnh)
EC = EM (gt)
⇒ ΔACE = ΔBME (c.g.c)
⇒ ∠ACE = ∠BME (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong ⇒ AC // MB
b) Xét ΔANF và ΔCBF có:
AF = CF (F là trung điểm của AC)
∠AFN = ∠CFB (2 góc đối đỉnh)
FN = FB (gt)
⇒ ΔANF = ΔCBF (c.g.c)
⇒ ∠ANF = ∠CBF (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong ⇒ AN // BC (1)
Xét ΔAME và ΔBCE có:
AE = BE (E là trung điểm của AB)
∠AEM = ∠BEC (2 góc đối đỉnh)
EM = EC (gt)
⇒ ΔAME = ΔBCE (c.g.c)
⇒ ∠AME = ∠BCE (2 góc tương ứng)
mà 2 góc ở vị trí so le trong ⇒ AM // BC (2)
Từ (1) và (2) ⇒ 3 điểm M, A, N thẳng hàng
c) Ta có: ΔANF = ΔCBF (theo b)
⇒ AN = BC (2 cạnh tương ứng) (3)
Ta có: ΔAME = ΔBCE (theo b)
⇒ AM = BC (2 cạnh tương ứng) (4)
Từ (3) và (4) ⇒ AM = AN
 Nhãn
Nhãn
a: Xét ΔAOB và ΔEOC có
OA=OE
\(\widehat{AOB}=\widehat{EOC}\)
OB=OC
Do đó: ΔAOB=ΔEOC
b: Xét tứ giác ABEC có
O là trung điểm của AE
O là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB=EC và AB//EC