Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tham khảo nha
https://hoc24.vn/cau-hoi/cho-ba-so-thuc-abc-duong-chung-minh-rangsqrtdfraca3a3leftbcright3sqrtdfracb3b3leftcaright3sqrtdfracc3c.5222680437292

Ta có:
\(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=9\\ \Leftrightarrow a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ac}=9\\ \Leftrightarrow\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=2\)
\(\Rightarrow\dfrac{\sqrt{a}}{a+2}+\dfrac{\sqrt{b}}{b+2}+\dfrac{\sqrt{c}}{c+2}=\dfrac{\sqrt{a}}{a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}+\dfrac{\sqrt{b}}{b+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}+\dfrac{\sqrt{c}}{c+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}}\\ =\dfrac{\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)}+\dfrac{\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)}+\dfrac{\sqrt{c}}{\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{\sqrt{a}\left(\sqrt{b}+\sqrt{c}\right)+\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)+\sqrt{c}\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{a}+\sqrt{c}\right)}\\ =\dfrac{4}{\sqrt{\left(\sqrt{a}+\sqrt{b}\right)^2\left(\sqrt{b}+\sqrt{c}\right)^2\left(\sqrt{a}+\sqrt{c}\right)^2}}\)\(=\dfrac{4}{\sqrt{\left(a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\left(b+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\left(c+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}}\\ =\dfrac{4}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}\)

Thử với \(a=b=c=0.1\), BĐT trở thành \(\dfrac{1}{10}\ge1\Rightarrow\) đề sai
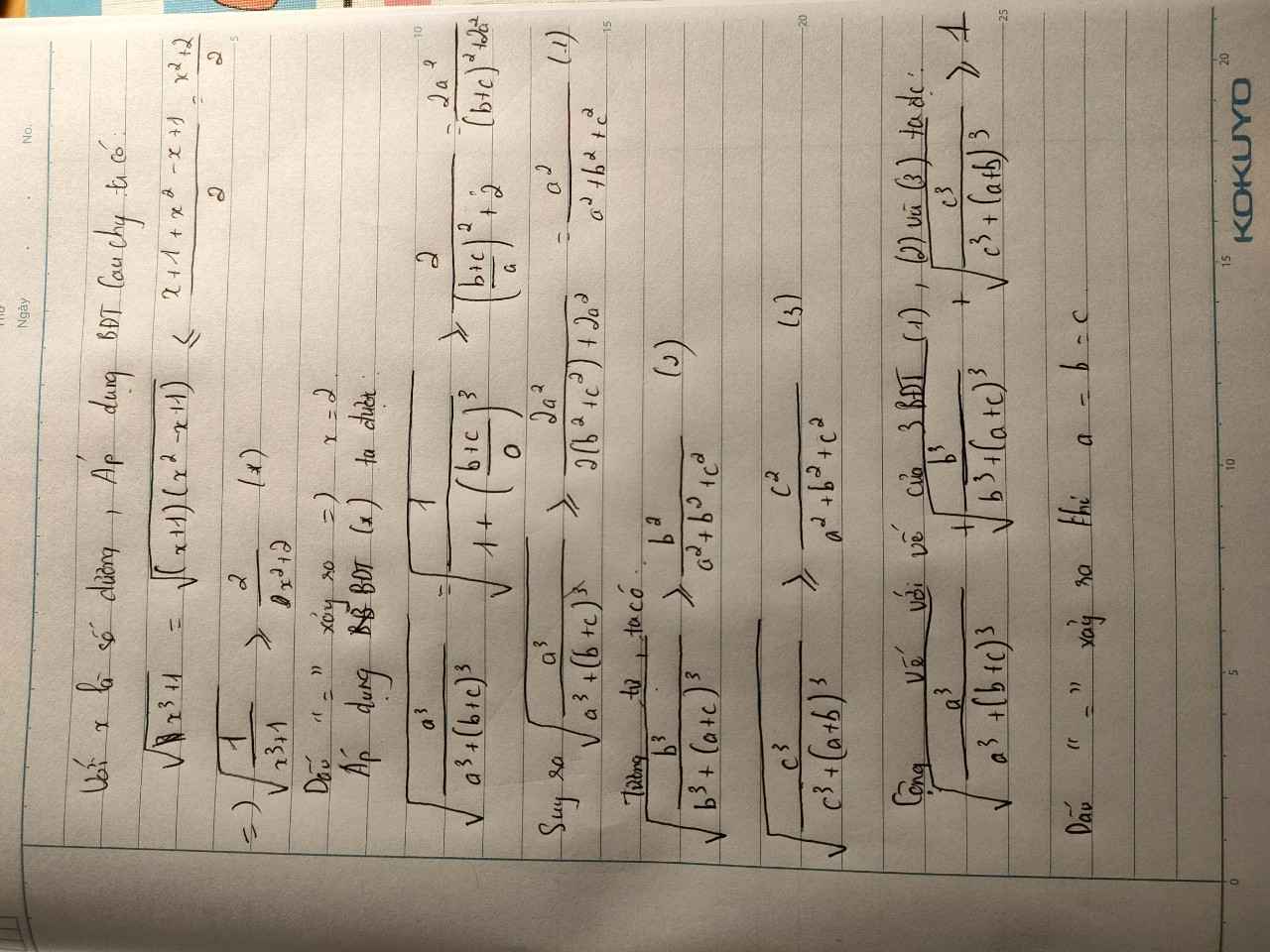
\(\Sigma\sqrt{\dfrac{a^3}{a^3+\left(b+c\right)^3}}=\Sigma\sqrt{\dfrac{1}{1+\left(\dfrac{b+c}{a}\right)^3}}\)\(\left(1\right)\)
\(đặt:\left(\left(\dfrac{b+c}{a}\right)^{ };\left(\dfrac{c+a}{b}\right)^{ };\left(\dfrac{a+b}{c}\right)^{ }\right)=\left(x;y;z\right)\)
\(\left(1\right)\Leftrightarrow\sqrt{\dfrac{1}{1+x^3}}+\sqrt{\dfrac{1}{1+y^3}}+\sqrt{\dfrac{1}{1+z^3}}=\sqrt{\dfrac{1}{\left(x+1\right)\left(x^2-x+1\right)}}+\sqrt{\dfrac{1}{\left(y+1\right)\left(y^2-y+1\right)}}+\sqrt{\left(z+1\right)\left(z^2-z+1\right)}\)
\(\sqrt{\dfrac{1}{\left(x+1\right)\left(x^2-x+1\right)}}\ge\dfrac{1}{\dfrac{x+1+x^2-x+1}{2}}=\dfrac{2}{x^2+2}\)
\(tương\) \(tự\Rightarrow\left(1\right)\ge\dfrac{2}{x^2+2}+\dfrac{2}{y^2+2}+\dfrac{2}{z^2+2}\)
\(=\dfrac{2}{\left(\dfrac{b+c}{a}\right)^2+2}+\dfrac{2}{\left(\dfrac{c+a}{b}\right)^2+2}+\dfrac{2}{\left(\dfrac{a+b}{c}\right)^2+2}=\dfrac{2a^2}{\left(b+c\right)^2+2a^2}+\dfrac{2b^2}{\left(c+a\right)^2+2b^2}+\dfrac{2c^2}{\left(a+b\right)^2+2c^2}\)
\(bunhia\Rightarrow\left(b+c\right)^2\le2\left(b^2+c^2\right)\Rightarrow\dfrac{2a^2}{\left(b+c\right)^2+2a^2}\ge\dfrac{2a^2}{2\left(a^2+b^2\right)+2a^2}=\dfrac{a^2}{a^2+b^2+c^2}\)
\(tương\) \(tự\Rightarrow\left(1\right)\ge\dfrac{a^2+b^2+c^2}{a^2+b^2+c^2}=1\left(đpcm\right)\)