Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét 2 tam giác vuông ΔABD và ΔACE có:
AB = AC (gt);
góc A chung
⇒ ΔABD = ΔACE (cạnh huyền - góc nhọn) (đpcm)
b, ΔABD = ΔACE ⇒ AD = AE
⇒ AC - AD = AB - AE ⇒ BE = CD
Xét 2 tam giác vuông ΔBIE và ΔCID có:
BE = CD
\(\widehat{BEI}=\widehat{CDI}\) ( đối đỉnh )
⇒ ΔBEI = ΔCDI (cạnh góc vuông - góc nhọn)

bạn không được nói vậy , nói thế là khinh người khác và đây là nơi chúng ta giao lưu giúp nhau mà , nên bạn không được nói bậy như thế.

a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
Suy ra: BE=CD
b: Ta có: ΔEBC=ΔDCB
nên \(\widehat{ECB}=\widehat{DBC}\)
hay ΔIBC cân tại I
Ta có: AE+EB=AB
AD+DC=AC
mà AB=AC
và EB=DC
nên AE=AD
Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại I
Do đó: I là trực tâm của ΔABC
Suy ra: AI\(\perp\)BC
mà AK\(\perp\)BC
nên A,I,K thẳng hàng
=>AK,BD,CE đồng quy

Xét tam giácBCE= tam giác CBD (cạnh huyền -mgóc nhọn)
góc ABC = góc ACB ( cân tại A)
BC chung
==> BD=CE
b) Tam giác BCE=tam giác CBD chứng minh ở câu a nên
góc BCE = góc DBC
--> IBC cân tại I

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔAED có AE=AD
nên ΔAED cân tại A
c: Xét ΔEBI vuông tại E và ΔDCI vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó; ΔEBI=ΔDCI
Suy ra: IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC

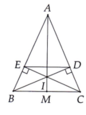
A B C E D M I
a) Xét \(\Delta BEC,\Delta DCB\) có:
\(\widehat{EBC}=\widehat{DCB}\) (ΔABC cân tại A)
\(BC:Chung\)
\(\widehat{BEC}=\widehat{CDB}\left(=90^o\right)\)
=> \(\Delta BEC=\Delta DCB\) (cạnh huyền - góc nhọn)
=> \(BE=CD\) (2 cạnh tương ứng)
Xét \(\Delta AEC,\Delta ADB\) có:
\(\widehat{A}:Chung\)
\(AB=AC\) (ΔABC cân tại A)
\(\widehat{AEC}=\widehat{ADB}\left(=90^{^O}\right)\)
=> \(\Delta AEC=\Delta ADB\) (cạnh huyền - góc nhọn)
=> \(AE=AD\) (2 cạnh tương ứng)
b) Xét \(\Delta AEI,\Delta ADI\) có :
\(AE=AD\)(cmt)
\(\widehat{AEI}=\widehat{ADI}\left(=90^o\right)\)
\(AI:Chung\)
=> \(\Delta AEI=\Delta ADI\left(c.g.c\right)\)
c) Từ \(\Delta AEI=\Delta ADI\left(cmt\right)\) suy ra :
\(\widehat{EAI}=\widehat{DAI}\) (2 góc tương ứng)
Do đó, AI là tia phân giác của \(\widehat{BAC}\)
d) Xét \(\Delta BEI,\Delta CDI\) có :
\(\widehat{BEI}=\widehat{CDI}\left(=90^o\right)\)
\(BE=CD\) (chứng minh câu a)
\(\widehat{BIE}=\widehat{CID}\) (đối đỉnh)
=> \(\Delta BEI=\Delta CDI\left(g.c.g\right)\)
e) Từ \(\Delta BEC=\Delta DCB\) (câu a) suy ra :
\(\widehat{ECB}=\widehat{DBC}\) (2 góc tương ứng)
Hay : \(\widehat{IBC}=\widehat{ICB}\)
Do đó, \(\Delta IBC\) cân tại I (đpcm)
f) Xét \(\Delta ABM,\Delta ACM\) có :
\(AB=AC\) (ΔABC cân tại A)
\(AM:Chung\)
\(BM=CM\) (M là trung điểm của BC)
=> \(\Delta ABM=\Delta ACM\left(c.c.c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> AM là tia phân giác của \(\widehat{BAC}\)
Lại có : AI là tia phân giác của \(\widehat{BAC}\) (chứng minh câu c)
Do đó : A, I ,M thẳng hàng (đpcm)

Điểm F ở đâu vậy bạn?
cái này là ace nhá
ko phải là afe