Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác ABC cân tại A nên góc B= góc C
theo bài ta co: BK.CH=BI^2=BI.CI => BI/BK = CH/ CI (BI=CI)
xét tam giác KBI và ICH có: góc B= góc C; BI/BK = CH/ CI
suy ra 2 tam giấc đồng dạng theo TH c.g.c.
b. từ a suy ra IK/IH = BK/CI = BK/BI (CI=BI)
và góc BKI= góc CIH.
ta có: KIB+B+BKI = 180
KIB+KIH+CIH = 180
suy ra góc B = góc KIH.
xét tam giác KIH và tam giAC KBI có:
góc B = góc I
IK/IH = BK/BI ( chứng minh trên )
suy ra 2 tam giác đồng dạng theo TH c.g.c
c. theo b suy ra góc IKH = góc BKI suy ra KI là phân giác góc BKH
d. theo c ta có IK/IH= BK/BI => IH. KB = IK. BI
tam giác KBI đồng dạng ICH => IK/IH = BI/CH => HC.IK = IH.BI
suy ra VT = IK.BI + IH. BI = BI.(IK+IH) > BI.HK ( theo bất đẳng thức tam giác: Tổng 2 cạnh trong tam giác lớn hơn cạnh còn lại)

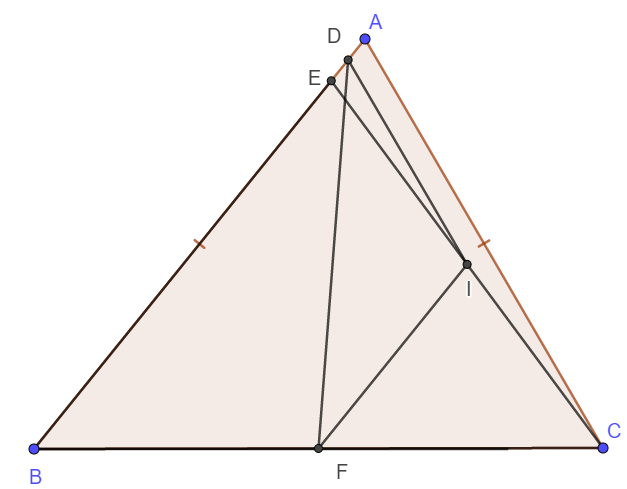
a) Xét tam giác ECB có I, F lần lượt là trung điểm của CE và CB nên IF là đường trung bình tam giác.
Suy ra \(IF=\frac{ED}{2}\)
Xét tam giác ECA có I, D lần lượt là trung điểm của CE và EA nên ID là đường trung bình tam giác.
Suy ra \(ID=\frac{AC}{2}\)
Mà AC = BE nên ID = IF
Vậy tam giác DIF cân tại I.
b) Do tam giác DIF cân tại I nên \(\widehat{FDI}=\widehat{DFI}\)
Lại có IF là đường trung bình tam giác BEC nên IF // AB, suy ra \(\widehat{DFI}=\widehat{FDB}\)
Từ đó ta có: \(\widehat{FDI}=\widehat{FDB}\Rightarrow\widehat{BDI}=2\widehat{IDF}\)
Cũng do DI là đường trung bình nên DI // AC hay \(\widehat{BDI}=\widehat{BAC}\)
Vậy nên \(\widehat{BAC}=2\widehat{IDF}\)