K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

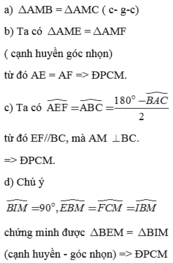
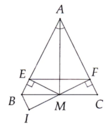
a. xét ∆AMB và ∆AMC, có:
AB = AC (∆ABC cân tại A)
\(\widehat{BAM}=\widehat{CAM}\) (AM là tia phân giác)
AM là cạnh chung
=> ∆AMB = ∆AMC (c-g-c)
b. xét ∆ vuông EAM và ∆ vuông FAM, có:
\(\widehat{EAM}=\widehat{FAM}\) (AM là tia phân giác)
AM là cạnh chung
=> △EAM = △FAM (ch-gn)
=> AE = AF (2 cạnh tương ứng)
=> △AEF là △ cân tại A
c. vì △EAM = △FAM (câu b)
nên AE = AF, ME = MF (2 cạnh tương ứng)
=> AM là đường trung trực của đoạn thẳng EF
=> AM vuông góc với EF
d. vì BI // AC => \(\widehat{AFM}=\widehat{BIM}=90^0\left(\text{so le trong}\right)\)
và \(\widehat{ACB}=\widehat{CBI}\) (so le trong)
xét △ vuông MEB và △ vuông MIB , có:
BM là cạnh chung
\(\widehat{MBE}=\widehat{MBI}\left(\text{cùng bằng }\widehat{ACB}\right)\)
=> △MEB = △MIB (ch - gn)
=> BE = BI (2 cạnh tương ứng)
cho cả hình đc ko