Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A E D B C
a) Xét \(\Delta EBC\)và \(\Delta DCB\)có:
C = B, CB chung, EBC = DCB \(\Rightarrow\) \(\Delta EBC\)= \(\Delta DCB\)\(\Rightarrow\)EC = DB
\(\Rightarrow\)AE = AD \(\Rightarrow\)\(\Delta AED\)cân.
b) Ta có:
C = \(\frac{180^o-A}{2}\), E = \(\frac{180^o-A}{2}\)\(\Rightarrow\)C = E \(\Rightarrow\)DE // BC ( đồng vị )
c) Vì \(\Delta EBC\)= \(\Delta DCB\)\(\Rightarrow\)BE = DC

a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)

a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
tham khảo á
làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50

a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
EBC = DCB (cmt)
BC là cạnh chung
ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180o - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180o - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
c) bớt ED đi, c/m ở trên r`
a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
EBC = DCB (cmt)
BC là cạnh chung
ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180o - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180o - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
c) bớt ED đi, c/m ở trên r`

A A A B B B C C C D D D E E E 1 2 1 2 1
a) BD và CE theo thứ tự là phân giác của góc B và góc C (gt) nên \(\widehat{B_1}=\widehat{B_2}=\frac{1}{2}\widehat{B},\widehat{C_1}=\widehat{C_2}=\frac{1}{2}\widehat{C}\)
mà \(\widehat{B}=\widehat{C}\)(hai góc ở đáy của \(\Delta\)cân ABC)
do đó \(\widehat{B_1}=\widehat{C_2}\)
\(\widehat{A}\)chung
=> \(\Delta\)ABD = \(\Delta\)ACE(g.c.g)
=> AD = AE(hai cạnh tương ứng)
=> \(\Delta\)ADE cân ở A
b) \(\Delta\)AED cân tại đỉnh A nên \(\widehat{AED}=\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\left(1\right)\)
\(\Delta\)ABC cân tại đỉnh A nên \(\widehat{ABC}=\widehat{ACB}=\frac{180^0-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{AED}=\widehat{ABC}\)
Vậy DE // BC(hai góc so le trong) mà \(\widehat{B_1}=\widehat{B_2}\), do đó \(\widehat{A}=60^0\), \(\widehat{D_1}=\widehat{B_2}\)=> \(\Delta\)BED cân ở đỉnh E,do đó BE = ED(3)
c) \(\Delta\)AEC cân tại đỉnh A nên \(\widehat{AEC}=\widehat{ACE}=\frac{180^0-\widehat{A}}{2}\)
\(\Delta\)ABD cân tại đỉnh A nên \(\widehat{ABD}=\widehat{ADB}=\frac{180^0-\widehat{A}}{2}\)
=> \(\widehat{AEC}=\widehat{ABD}\)
=> CE // BD(hai góc so le trong)
Mà \(\widehat{C_1}=\widehat{C_2}\),do đó \(\widehat{A}=60^0,\widehat{D_1}=\widehat{C_2}\)
=> \(\Delta\)CED cân ở đỉnh D nên ED = DC(4)
Từ (3) và (4) => BE = ED = DC

a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)

a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)

a: Xét ΔABC có BD là đường phân giác
nên AB/BC=AD/DC
=>AD/DC=AC/BC(1)
Xét ΔABC có CE là đường phân giác
nên AE/EB=AC/BC(2)
Từ (1) và (2) suy ra AD/DC=AE/EB
=>ED//BC
=>\(\widehat{EDB}=\widehat{DBC}\)
mà \(\widehat{DBC}=\widehat{EBD}\)
nên \(\widehat{EDB}=\widehat{EBD}\)
b: Xét ΔABC có DE//BC
nên AE/AB=AD/AC
mà AB=AC
nên AE=AD
hay ΔADE cân tại A
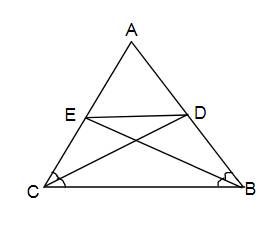
a: Ta có: \(\widehat{ABD}=\widehat{DBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Xét ΔABC có \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
nên DE//BC
c: Sửa đề: BE=ED=DC
Ta có: ED//BC
=>\(\widehat{EDB}=\widehat{DBC}\)(hai góc so le trong)
mà \(\widehat{DBC}=\widehat{EBD}\)(BD là phân giác của góc EBC)
nên \(\widehat{EDB}=\widehat{EBD}\)
=>ΔEBD cân tại E
=>EB=ED
Ta có: AE+EB=AB
AD+DC=AC
mà AE=AD
và AB=AC
nên EB=DC
=>BE=ED=DC