
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao

a: \(\widehat{ABC}=\widehat{C}\)(vì ΔABC cân tại A)
b: AB>AD vì \(\widehat{ADB}\) là góc tù

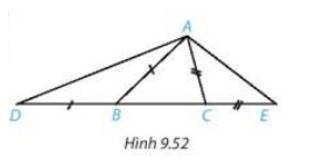
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).

Bài 1 a, xét tam giác ABD và tam giác HBD có:
BD cạnh chung
\(\widehat{ABD}\)=\(\widehat{HBD}\)(gt)
\(\Rightarrow\)tam giác ABD = tam giác HBD( CH-GN)
\(\Rightarrow\)AB=HB
b,trên tia đối của tia DH lấy O sao cho HD=DO
xét tam giác ADO và tam giác CDH có:
DH=DO( theo trên)
\(\widehat{ADO}\)=\(\widehat{CDH}\)( Vì đối đỉnh)
\(\Rightarrow\)tam giác ADO=tam giác CDH( CH-GN)\(\Rightarrow\)AD=CD

e nằm giữa A và C nên AE< AC \(\Rightarrow\)BE<BC( đường xiên nào có hình chiếu lớn hơn thì lớn hơn)
do tam giác ABC vuông tại A nên BA là đường vuông góc nên BA là đường thẳng ngắn nhất \(\Rightarrow\)BA<BE
Vậy BA<BE<BC
làm tương tự phần b
*) Trường hợp 1: \(D\equiv H\)
AD là đường vuông góc, AB là đường xiên hạ từ A xuống BC nên AB > AD (1)
*) Trường hợp 2:
\(D\ne H\) \(\Rightarrow D\) nằm giữa BH hoặc CH
+) D nằm giữa BH và giả sử \(D\equiv D_1\)
Ta có:
\(\widehat{AD_1B}\) là góc ngoài của \(\Delta AHD_1\)
\(\Rightarrow\widehat{AD_1B}=\widehat{D_1AH}+\widehat{AHD_1}\)
\(\Rightarrow\widehat{AD_1B}\) là góc tù nên là góc lớn nhất trong \(\Delta ABD_1\)
Mà AB là cạnh đối diện với \(\widehat{AD_1B}\) nên AB là cạnh lớn nhất
\(\Rightarrow AB>AD_1\)
\(\Rightarrow AB>AD\) (2)
+) D nằm giữa CH và giả sử \(D\equiv D_2\)
Ta có:
\(\widehat{AD_2C}\) là góc ngoài của \(\Delta AHD_2\)
\(\Rightarrow\widehat{AD_2C}=\widehat{D_2AH}+\widehat{AHD_2}\)
\(\Rightarrow\widehat{AD_2C}\) là góc tù nên là góc lớn nhất trong \(\Delta ACD_2\)
Mà AC là cạnh đối diện với \(\widehat{AD_2C}\) nên AC là cạnh lớn nhất
\(\Rightarrow AC>AD_2\)
\(\Rightarrow AC>AD\)
Mà AB = AC (\(\Delta ABC\) cân tại A)
\(\Rightarrow AB>AD\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow AB>AD\)