Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a
XÉT ΔAHB VÀ ΔDBH
BH- CẠNH CHUNG
^AHB=^DBH
AH=BD
=>ΔAHB = ΔDBH (CGC)
B) VÌ ΔAHB = ΔDBH
=> ^ABH=^DHB
MÀ 2 GÓC NÀY Ở T SO LE TRONG CỦA AB VÀ HD
=>AB//HD
C)
VÌ ΔAHB = ΔDBH
=>AB=DH (2CTU)
=>AC=BD(2CTU)
XÉT TAM GIÁC BAD VÀ TAM GIÁC HAD P/S : CÓ AI ĐỂ Ý 2 TỪ TA BAD VÀ HADKO ;V
AB=DH
AC=BD
AD-CẠNH CHUNG
=>TAM GIÁC BAD = TAM GIÁC HAD
=>^BAD=^HDA
=> ^BAO=^ODH
XÉT TAM GIÁC BAO VÀ TAM GIÁC HDO
^BAD=^HDA
AB=HD
^BAO=^ODH
=> TAM GIÁC BAO = TAM GIÁC HDO
=> BO=HO (2CTU)
=> O là trung điểm của BH

a) Vì tg ABC cân=> ^ABC = ^ACB mà 180-ABC=ABD và 180-ACB=ACE
=> ^ABD = ^ACE
TG ABD = TG ACE (c.g.c)
=> ABD=ACE => TG ADE cân(đpcm)
b) * CM được TG HBD = TG KCE (cạnh huyền- góc nhọn)
=> BH=CK (đpcm)
=> DH=KE
* Ta có: AD = AE (vì TG ADE cân)
DH=KE(CMT)
mà AD - DH = AH
AE - KE = AK
=> AH = AK
và DH=KE ( CMT)
Do đó: HK là đường trung bình của TG ADE
=> HK // DE
c, ý b là BOC?
^HBD=^KCE (TG HBD= TG KCE )
=> ^CBO = ^BCO (đối đỉnh vs 2 góc = nhau)
=> TG OBC cân
*

1:
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
AB=CD
\(\widehat{OBA}=\widehat{ODC}\)(hai góc so le trong, AB//CD)
Do đó: ΔOAB=ΔOCD
=>OA=OC và OB=OD
=>O là trung điểm chung của AC và BD
b: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
OD=OB
Do đó: ΔOAD=ΔOCB
=>\(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
c: ΔOAD=ΔOCB
=>AD=BC
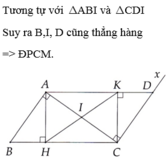
2:
a: Xét ΔAHO vuông tại H và ΔCKO vuông tại K có
OA=OC
\(\widehat{AOH}=\widehat{COK}\)
Do đó: ΔAHO=ΔCKO
=>AH=CK và OH=OK
b: Xét ΔAOK và ΔCOH có
OA=OC
\(\widehat{AOK}=\widehat{COH}\)
OK=OH
Do đó; ΔAOK=ΔCOH
=>\(\widehat{OAK}=\widehat{OCH}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AK//CH
c: OH=OK
H,O,K thẳng hàng
Do đó: O là trung điểm của HK
d: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
=>AE//CF
Xét tứ giác AECF có
AE//CF
AF//CE
Do đó: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nen O là trung điểm của EF
3: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
4: Xét ΔOIB và ΔOVD có
\(\widehat{IBO}=\widehat{VDO}\)
OB=OD
\(\widehat{IOB}=\widehat{VOD}\)
Do đó: ΔOIB=ΔOVD
=>BI=DV