Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: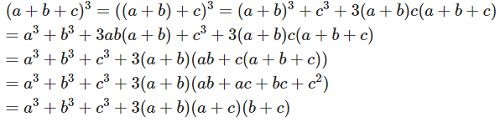
\(\Rightarrow3\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a+b=0\\b+c=0\\c+a=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-b,c=-1\\b=-c,a=-1\\c=-a,b=-1\end{matrix}\right.\)
Trường hợp a = -b
\(\Rightarrow a^{2019}+b^{2019}+c^{2019}=\left(-b\right)^{2019}+b^{2019}+c^{2019}=c^{2019}=\left(-1\right)^{2019}=-1\)
Các trường hợp khác tương tự đều có kq = -1

<=> \(2a^2+2b^2+2c^2=2ab+2bc+2ca< =>\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0< =>\)
a=b=c => 32020 = 3.a2019 <=> 32019 = a2019 => a=b=c=3
A= 12017 + 02018 + (-1)2019 = 0

\(a+b=c+\frac{1}{2019}\Leftrightarrow a+b-c=\frac{1}{2019}\Leftrightarrow\frac{1}{a+b-c}=2019\)
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{c}+2019\Rightarrow\frac{1}{a}+\frac{1}{b}-\frac{1}{c}=2019\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}-\frac{1}{c}=\frac{1}{a+b-c}\Rightarrow\frac{1}{a}+\frac{1}{b}=\frac{1}{a+b-c}+\frac{1}{c}\)
\(\Leftrightarrow\frac{a+b}{ab}=\frac{a+b}{c\left(a+b-c\right)}\Leftrightarrow c\left(a+b-c\right)\left(a+b\right)=\left(a+b\right)ab\)
\(\Leftrightarrow c\left(a+b-c\right)\left(a+b\right)-ab\left(a+b\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(ca+bc-c^2-ab\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left[c\left(a-c\right)-b\left(a-c\right)\right]=0\)
\(\Leftrightarrow\left(a+b\right)\left(c-b\right)\left(a-c\right)=0\)
=>a=-b hoặc c=b hoặc a=c
không mất tính tổng quát, giả sử a=-b, ta có:
\(P=\left(-b^{2019}+b^{2019}-c^{2019}\right)\left(-\frac{1}{b^{2019}}+\frac{1}{b^{2019}}-\frac{1}{c^{2019}}\right)=\left(-c\right)^{2019}\cdot\left(\frac{-1}{c}\right)^{2019}=1\)
tương tư với các trường hợp khác ta cũng có P=1
Vậy P=1

\(a^3+1+1\ge3\sqrt[3]{a^3.1.1}=3a\)
Thiết lập tương tự hai BĐT còn lại và cộng theo vế,ta có:
\(a^3+b^3+c^3+6\ge3\left(a+b+c\right)\)
\(\Leftrightarrow a^3+b^3+c^3+6\ge39\)
\(\Leftrightarrow a^3+b^3+c^3\ge33\)
Mà theo đề bài \(a^3+b^3+c^3=27< 33\rightarrow\)vô lí.
Do đó đề sai!