AW
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 10 2022
Bài 4:
=>x(x^2+1)=0
=>x=0
Bài 5:
=>\(3n^3+n^2+9n^2-1-4⋮3n+1\)
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Bài 3:
\(a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)
21 tháng 5 2022
Bài 2:
\(\left(a+b+c\right)^2=3\left(ab+bc+ac\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-3ab-3ac-3bc=0\)
\(\Leftrightarrow a^2+b^2+c^2-ab-bc-ac=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>a=b=c
4 tháng 4 2020
a/CM: \(\left(\frac{a+b}{2}\right)^2\ge ab\)
\(\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
\(\Leftrightarrow a+b\ge2\sqrt{ab}\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) ( luôn đúng với mọi a,b>0)
CM: \(\frac{a^2+b^2}{2}\ge\left(\frac{a+b}{2}\right)^2\)
\(\Leftrightarrow\frac{2\left(a^2+b^2\right)}{4}\ge\frac{\left(a+b\right)^2}{4}\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow a^2+b^2\ge2ab\) ( luôn đúng)
b/CM: \(\frac{a^3+b^3}{2}\ge\left(\frac{a+b}{2}\right)^3\)
\(\Leftrightarrow\frac{4\left(a^3+b^3\right)}{8}\ge\frac{\left(a+b\right)^3}{8}\)
\(\Leftrightarrow3\left(a^3+b^3\right)\ge3a^2b+3ab^2\)
\(\Leftrightarrow a^2\left(a-b\right)+b^2\left(b-a\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2-b^2\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\) ( luôn đúng với mọi a,b>0)
c/CM: \(a^4+b^4\ge a^3b+ab^3\)
\(\Leftrightarrow a^3\left(a-b\right)-b^3\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+b^2+ab\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+\frac{2ab}{2}+\frac{b^2}{4}+\frac{3b^2}{4}\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(\left(a+\frac{b}{2}\right)^2+\frac{3b^2}{4}\right)\ge0\) ( luôn đúng)
d/Ta xét hiệu: \(a^4-4a+3\)
\(=a^4-2a^2+1+2a^2-4a+2\)
\(=\left(a-1\right)^2+2\left(a-1\right)^2\ge0\)
Suy ra BĐT luôn đúng
e/Ta xét hiệu:( Làm nhanh)
\(a^3+b^3+c^3-3abc\)\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
\(=\frac{1}{2}\left(a+b+c\right)\left(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right)\ge0\)
f/Ta có: \(\frac{a^6}{b^2}-a^4+\frac{a^2b^2}{4}+\frac{b^6}{a^2}-b^4+\frac{a^2b^2}{4}\)
\(=\left(\frac{a^3}{b}-\frac{ab}{2}\right)^2+\left(\frac{b^3}{a}-\frac{ab}{2}\right)^2\ge0\)(1)
Mà \(\frac{a^2b^2}{4}+\frac{a^2b^2}{4}\ge0\)(2)
Lấy (1) trừ (2) được: \(\frac{a^6}{b^2}+\frac{b^6}{a^2}-a^4-b^4\ge0\RightarrowĐPCM\)
g/Làm rồi..xem lại trong trang cá nhân
h/Xét hiệu có: \(\left(a^5+b^5\right)\left(a+b\right)-\left(a^4+b^4\right)\left(a^2+b^2\right)\)
\(=a^5b+ab^5-a^2b^4-a^4b^2\)
\(=a^4b\left(a-b\right)-ab^4\left(a-b\right)\)
\(=ab\left(a^2-b^2\right)\left(a-b\right)\)
\(=ab\left(a+b\right)\left(a-b\right)^2\ge0\forall ab>0\)
Suy ra ĐPCM
DA
20 tháng 10 2018
Bài 1: theo mình nghĩ thì nên cho thêm điều kiện gì chứ ạ :(
Bài 2: Ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{1}{c}\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^3=\left(-\dfrac{1}{c}\right)^3\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+3.\dfrac{1}{ab}.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=-\dfrac{1}{c^3}\) ( hằng đẳng thức: \(\left(a+b\right)^3=a^3+b^3+3ab\left(a+b\right)\) )
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=-3.\dfrac{1}{ab}.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=-3.\dfrac{1}{ab}.\left(-\dfrac{1}{c}\right)\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
Có \(A=\dfrac{bc}{a^2}+\dfrac{ca}{b^2}+\dfrac{ab}{c^2}\)
\(A=abc\left(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\right)\)
\(A=abc.\dfrac{3}{abc}=3\)
Bải 3: Ta có
\(x+y+z=0\)
\(\Rightarrow y+z=-x\)
\(\Rightarrow\left(y+z\right)^5=-x^5\)
\(\Rightarrow y^5+5y^4z+10y^3z^2+10y^2z^3+5yz^4+z^5+x^5=0\)
\(\Rightarrow x^5+y^5+z^5+5yz\left(y^3+2y^2z+2yz^2+z^3\right)=0\)
\(\Rightarrow x^5+y^5+z^5+5yz\left[\left(y+z\right)\left(y^2-yz+z^2\right)+2yz\left(y+z\right)\right]=0\)
\(\Rightarrow x^5+y^5+z^5+5yz\left(y+z\right)\left(y^2-yz+z^2+2yz\right)=0\)
\(\Rightarrow x^5+y^5+z^5+5yz\left(y+z\right)\left(y^2+yz+z^2\right)=0\)
\(\Rightarrow x^5+y^5+z^5=-5yz\left(y+z\right)\left(y^2+yz+z^2\right)=0\)
\(\Rightarrow2\left(x^5+y^5+z^5\right)=2.-5yz.\left(-x\right)\left(y^2+yz+z^2\right)\)
\(\Rightarrow2.\left(x^5+y^5+z^5\right)=5xyz.\left(2y^2+2yz+2z^2\right)\)
\(\Rightarrow2\left(x^5+y^5+z^5\right)=5xyz\left[\left(y+z\right)^2+y^2+z^2\right]\)
\(\Rightarrow2\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
AH
Akai Haruma
Giáo viên
30 tháng 10 2019
Bài 1:
\(x^2+y^2-2x-4y+5=0\)
\(\Leftrightarrow (x^2-2x+1)+(y^2-4y+4)=0\)
\(\Leftrightarrow (x-1)^2+(y-2)^2=0\)
Vì $(x-1)^2; (y-2)^2\geq 0$ với mọi $x,y\in\mathbb{R}$ nên để tổng của chúng bằng $0$ thì $(x-1)^2=(y-2)^2=0$
$\Rightarrow x=1; y=2$
Vậy...........
AH
Akai Haruma
Giáo viên
30 tháng 10 2019
Bài 2:
Ta có:
\(a(a-b)+b(b-c)+c(c-a)=0\)
\(\Leftrightarrow 2a(a-b)+2b(b-c)+2c(c-a)=0\)
\(\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2)=0\)
\(\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0\)
Lập luận tương tự bài 1, ta suy ra :
\((a-b)^2=(b-c)^2=(c-a)^2=0\Rightarrow a=b=c\)
Khi đó, thay $b=c=a$ ta có:
\(P=a^3+b^3+c^3-3abc+3ab-3c+5\)
\(=3a^3-3a^3+3a^2-3a+5=3a^2-3a+5\)
\(=3(a^2-a+\frac{1}{4})+\frac{17}{4}=3(a-\frac{1}{2})^2+\frac{17}{4}\geq \frac{17}{4}\)
Vậy $P_{\min}=\frac{17}{4}$
Giá trị này đạt được tại $b=c=a=\frac{1}{2}$
PT
22 tháng 9 2017
1. \(a^3+b^3+c^3-3abc\)
\(=a^3+b^3+3a^2b+3ab^2-3a^2b-3ab^2+c^3-3abc\)
\(=\left(a+b\right)^3-3a^2b-3ab^2+c^3-3abc\)
\(=\left[\left(a+b\right)^3+c^3\right]-3ab.\left(a+b+c\right)\)
\(=\left(a+b+c\right).\left[\left(a+b\right)^2-c.\left(a+b\right)+c^2\right]-3ab.\left(a+b+c\right)\)
\(=\left(a+b+c\right).\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right).\left(a^2+b^2+c^2-bc-ab-ca\right)\)
Mà \(a+b+c=0\)
\(\Rightarrow\left(a+b+c\right).\left(a^2+b^2+c^2-bc-ab-ca\right)=0\)
\(\Rightarrow a^3+b^3+c^3-3abc=0\)
\(\RightarrowĐpcm.\)
2. Dễ rồi.
3.
\(A=2.\left(x-y\right).\left(x^2+xy+y^2\right)-3.\left(x^2+2xy+y^2\right)\)
\(A=4.\left(x^2+xy+y^2\right)-3x^2-6xy-3y^2\)
\(A=4x^2+4xy+4y^2-3x^2-6xy-3y^2\)
\(A=x^2-2xy+y^2\)
\(A=\left(x-y\right)^2\)
Thay \(x-y=2\) vào ta có:
\(A=\left(x-y\right)^2\)\(=2^2=4\)
4. \(A=x^2-3x+5\)
\(A=x^2-2.x.\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{11}{4}\)
\(A=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\)
\(\Rightarrow x-\dfrac{3}{2}=0\)
\(\Rightarrow x=\dfrac{-3}{2}\)
\(\Rightarrow Min_A=\dfrac{11}{4}\Leftrightarrow x=\dfrac{-3}{2}\)
\(B=\left(2x-1\right)^2+\left(x+2\right)^2\)
\(B=4x^2-4x+1+x^2+4x+4\)
\(B=5x^2+5\)
Ta có: \(5x^2\ge0\)
\(\Rightarrow5x^2+5\ge0\)
\(\Rightarrow Min_B=5\Leftrightarrow x=0\)
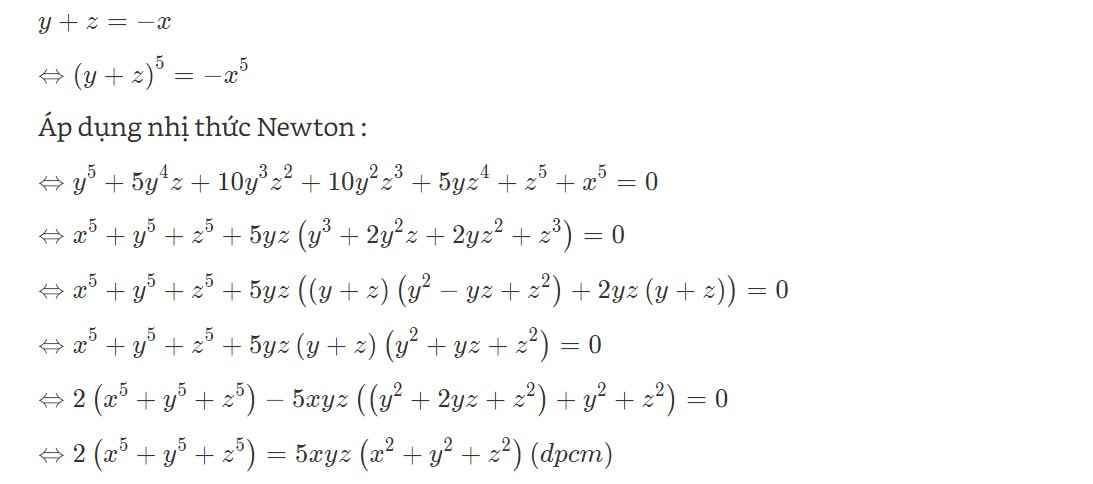
Xét hiệu
\(a^3-a^2+b^3-b^2+c^3-c^2=0\)
<=>\(a^2(a-1)+b^2(b-1)+c^2(c-1)=0\)
Ta có:\(a^2+b^2+c^2=1\)
=>\(a^2\le1\)
=>|a|\(\le1\)
Mà|a|\(\ge a\)
=>a \(\le1\)
=>\(a^2(a-1)\le0\)
CMTT:\(b^2(b-1)\le0\)
\(c^2(c-1)\le0\)
Mà \(a^2(a-1)+b^2(b-1)+c^2(c-1)=0\)
Dấu "=" xảy ra<=>a=1=>b=c=0
b=1=>a=c=0
c=1=>a=b=0
=>\(a^5+b^5+c^5=1\)