Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)
3 điểm M;A;B thẳng hàng khi:
\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)
\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)

Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5
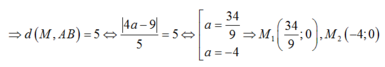

Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;4\right)\\\overrightarrow{DC}=\left(4-x;-1-y\right)\end{matrix}\right.\)
Do \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\left\{{}\begin{matrix}4-x=4\\-1-y=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-5\end{matrix}\right.\) \(\Rightarrow D\left(0;-5\right)\)
b/ Gọi pt AB có dạng \(y=ax+b\Rightarrow\left\{{}\begin{matrix}-a+b=-2\\3a+b=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\end{matrix}\right.\) \(\Rightarrow y=x-1\)
Giao với Ox: \(y=0\Rightarrow x=1\Rightarrow\left(1;0\right)\)
c/ Của đường thẳng y=2 với cái gì bạn?

Ủa, cái b2-3 và b2-4 kia là sao em?
Nó là \(b^2-3\) hay \(b_2-3\)?
Lời giải:
a. Gọi ptđt $AB$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -1=2a+b\\ 3=-5a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-4}{7}\\ b=\frac{1}{7}\end{matrix}\right.\)
Vậy ptđt $AB$ là $y=\frac{-4}{7}x+\frac{1}{7}$
$M\in Ox$ nên $y_M=0$
$M\in AB$ nên: $y_M=\frac{-4}{7}x_M+\frac{1}{7}$
$\Leftrightarrow 0=\frac{-4}{7}x_M+\frac{1}{7}$
$\Rightarrow x_M=\frac{1}{4}$
Vậy $M(\frac{1}{4}, 0)$
b. Gọi giao điểm của $Oy$ và $AB$ là $(0,a)$.
Do điểm này thuộc $AB$ nên:
$a=\frac{-4}{7}.0+\frac{1}{7}=\frac{1}{7}$
Vậy $(0,\frac{1}{7})$ là giao của $AB$ và trục $Oy$