Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vecto AB = (3 - m; 3 - 2m)
Vecto AC = (-2; 2)
A, B, C thẳng hàng
<=> vecto AB và vecto AC cùng phương
<=> (3 - m)/(-2) = (3 - 2m)/2
<=> m - 3 = 3 - 2m
<=> 3m = 6
=> m = 2
-> A

A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)


\(\overrightarrow{AB}\left(-3;2\right)\); \(\overrightarrow{AC}\left(1;m-2\right)\).
Ba điểm A, B, C thẳng hàng khi và chỉ khi:
\(\dfrac{1}{-3}=\dfrac{m-2}{2}\Leftrightarrow-3\left(m-2\right)=2\)\(\Leftrightarrow m=\dfrac{4}{3}\).

a.
\(A\cap B\cap C=\left[0;5\right]\)
Ý thứ 2 ko hiểu đề yêu cầu gì
b.
\(P\cap Q\ne\varnothing\Leftrightarrow\left\{{}\begin{matrix}m< 5\\m+4>-2\end{matrix}\right.\) \(\Rightarrow-6< m< 5\)
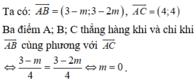

bn thiếu các dấu vec tơ nha
ta có : \(\overrightarrow{AB}\left(3-m;3-2m\right)\) và \(\overrightarrow{AC}\left(-2;2\right)\)
để : \(A;B;C\) thẳng hàng khi và chỉ khi \(\overrightarrow{AB}\) cùng phương với \(\overrightarrow{AC}\)
tương đương \(\dfrac{3-m}{-2}=\dfrac{3-2m}{2}\) \(\Leftrightarrow\dfrac{m-3}{2}=\dfrac{3-2m}{2}\)
\(\Leftrightarrow m-3=3-2m\Leftrightarrow3m=6\Leftrightarrow m=\dfrac{6}{3}=2\)
vậy \(m=2\) thì 3 điểm \(A;B;C\) thẳng hàng