Cho A = 4 x...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

29 tháng 4 2018

Cho A = 4 x 2 - 4 x + 1 4 x - 2 . Chứng minh |A| = 0,5 với x ≠ 0,5.

#Hỏi cộng đồng OLM #Toán lớp 9

Cao Minh Tâm

29 tháng 4 2018

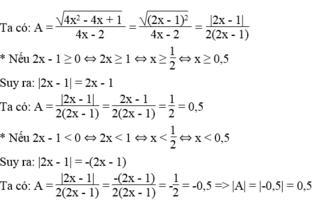
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Báo Mẫn

14 tháng 5 2019

Rút gọn các biểu thức sau :

a) \(\frac{x^2-4}{2}\sqrt{\frac{4}{x^2-4x+4}}\) với x khác 2

b) \(\frac{\sqrt{x^2+x+\frac{1}{4}}}{2x+1}\) với x khác -0,5

c) \(\frac{\sqrt{4x^2-4x+1}}{4x^2-1}\) với x khác 0,5 và -0,5

#Hỏi cộng đồng OLM #Toán lớp 9

14 tháng 5 2019

a) A \(=\frac{x^2-4}{2}\cdot\sqrt{\frac{2^2}{\left(x-2\right)^2}}\) \(=\frac{x^2-4}{2}\cdot\left|\frac{2}{x-2}\right|\)

+ Với x < 2 ta có \(A=\frac{x^2-4}{2}\cdot\frac{2}{2-x}\)

\(A=\frac{\left(x+2\right)\left(x-2\right)}{2-x}=-\left(x+2\right)\)

+ Với x > 2 ta có : \(A=\frac{x^2-4}{2}\cdot\frac{2}{x-2}\)

\(A=\frac{\left(x-2\right)\left(x+2\right)}{x-2}=x+2\)

câu b và c tương tự

Đúng(0)

thắm nguyễn

26 tháng 10 2019 - olm

\(A= { \sqrt{4x^2-4x+1}}\) / 4X+2

chứng minh | A | =0,5 với x # 0,5

#Hỏi cộng đồng OLM #Toán lớp 9

Kathrine

25 tháng 12 2019

chưa học cái này

Đúng(0)

Sách Giáo Khoa

25 tháng 4 2017

Cho \(A=\dfrac{\sqrt{4x^2-4x+1}}{4x-2}\)

Chứng minh \(\left|A\right|=0,5\) với \(x\ne0,5\)

#Hỏi cộng đồng OLM #Toán lớp 9

Dennis

31 tháng 7 2017

A = \(\dfrac{\sqrt{4x^2-4x+1}}{4x-2}\)

A = \(\dfrac{\sqrt{\left(2x-1\right)^2}}{2\left(2x-1\right)}\)

A = \(\dfrac{\left|2x-1\right|}{2\left(2x-1\right)}\)

\(\left|A\right|=\dfrac{2x-1}{2\left(2x-1\right)}\) \(\Rightarrow\left|A\right|=\dfrac{1}{2}=0,5\left(x\ne0,5\right)\)

Đúng(0)

hằng đinh thị thu

22 tháng 10 2018

còn một phần câu trả lời nữa bạn ạ

Đúng(0)

Vũ Thị Chi

10 tháng 5 2018

Cho A = \(\dfrac{x-2}{2+\sqrt{x}}\) và B = \(\dfrac{4\left(2x-1\right)}{2x+1}\) với \(x>0\), x # \(\dfrac{1}{2}\), x # \(\dfrac{1}{4}\)

Chứng minh \(\dfrac{A}{B}=\dfrac{x-2}{4\sqrt{x}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

Doan Minh Cuong

12 tháng 5 2018

Đề bài sai: Khi \(x=4\) thì \(A=\dfrac{1}{2};B=\dfrac{28}{9};\dfrac{A}{B}=\dfrac{9}{56};\dfrac{x-2}{4\sqrt{x}}=\dfrac{1}{4}\Rightarrow\dfrac{A}{B}\ne\dfrac{x-2}{4\sqrt{x}}\)

Đúng(0)

nguyễn thị oanh

16 tháng 8 2016

Rút gọn biểu thức với điều kiện đã cho của x rồi tính giá trị của nó;

a) \(\sqrt{\frac{\left(x-2\right)^4}{\left(3-x\right)^2}}\)+\(\frac{x^2-1}{x-3}\) (x<3) ;tại x= 0,5

b) 4x -\(\sqrt{8}\)+\(\frac{\sqrt{x^3+2x^2}}{\sqrt{x+2}}\) (x>-2) ; tại x= -\(\sqrt{2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

Lightning Farron

16 tháng 8 2016

a)\(\sqrt{\frac{\left(x-2\right)^4}{\left(3-x\right)^2}}+\frac{x^2-1}{x-3}=\frac{\sqrt{\left(x-2\right)^4}}{\sqrt{\left(3-x\right)^2}}+\frac{x^2-1}{x-3}=\frac{\left(x-2\right)^2}{x-3}+\frac{x^2-1}{x-3}=\frac{x^2-4x+4+x^2-1}{x-3}=\frac{2x^2-4x+3}{x-3}\)

Tại x=0,5 thay vào ta có:

\(A=\frac{2\cdot\left(0,5\right)^2-4\cdot0,5+3}{0,5-3}=-\frac{3}{5}\)

b)\(4x-\sqrt{8}+\frac{\sqrt{x^3+2x^2}}{\sqrt{x+2}}=4x-\sqrt{8}+\frac{\sqrt{x^2\left(x+2\right)}}{\sqrt{x+2}}=4x-\sqrt{8}+\frac{\sqrt{x^2}\cdot\sqrt{x+2}}{\sqrt{x+2}}\)\(=4x-\sqrt{8}+x^2\)

Tại \(x=-\sqrt{2}\) thay vào ta có:

\(B=4\cdot\left(-\sqrt{2}\right)+\left(-\sqrt{2}\right)^2=2-4\sqrt{2}\)

Đúng(0)

Nguyen My

9 tháng 7 2019

Cho A=\(\frac{x^4+1}{\left(1+x^2\right)^2}\)

với x>0. Chứng minh \(A\ge\frac{1}{2}\)

#Hỏi cộng đồng OLM #Toán lớp 9

Mashiro Shiina

9 tháng 7 2019

Xét hiệu:

\(A=\frac{x^4+1}{\left(x^2+1\right)^2}-\frac{1}{2}=\frac{2\left(x^4+1\right)-\left(x^4+2x^2+1\right)}{2\left(x^2+1\right)^2}=\frac{x^4-2x^2+1}{2\left(x^2+1\right)^2}=\frac{\left(x^2-1\right)^2}{2\left(x^2+1\right)^2}\ge0\)Dấu bằng xảy ra khi x=1

Đúng(0)

phạm thị hồng anh

11 tháng 8 2016

Cho B=\(\sqrt{\frac{\left(x-2\right)^4}{\left(3-x\right)^2}}+\frac{x^2+1}{x-3}\)

a)Rut gon B khi x<3

b)Tinh B khi x=0,5

#Hỏi cộng đồng OLM #Toán lớp 9

Trần Việt Linh

11 tháng 8 2016

a) \(B=\sqrt{\frac{\left(x-2\right)^4}{\left(3-x\right)^2}}+\frac{x^2+1}{x-3}=\frac{\left(x-2\right)^2}{3-x}+\frac{x^2+1}{x-3}\\ =\frac{-\left(x-2\right)^2+x^2+1}{x-3}=\frac{-x^2+4x-4+x^2+1}{x-3}=\frac{4x-3}{x-3}\)

b) khi x=0,5 thì

\(B=\frac{4\cdot0,5-3}{0,5-3}=\frac{2}{5}\)

Đúng(0)

27 tháng 10 2020 - olm

Rút gọn biểu thức

a) \(\sqrt{12}-3\sqrt{75}+0,5\sqrt{\left(-6\right)^2\times3}\)

b) \(3\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}-\sqrt{4+2\sqrt{3}}\)

c) \(\left(\frac{2x+1}{x\sqrt{x}-1}-\frac{\sqrt{x}}{x+\sqrt{x}+1}\right):\frac{1}{x-2\sqrt{x}+1}\) (với \(x\ge0;x\ne1\))

#Hỏi cộng đồng OLM #Toán lớp 9

Nguyễn Minh Đăng

27 tháng 10 2020

a) \(\sqrt{12}-3\sqrt{75}+0,5\sqrt{\left(-6\right)^2\cdot3}\)

\(=2\sqrt{3}-15\sqrt{3}+0,5\sqrt{108}\)

\(=-13\sqrt{3}+3\sqrt{3}\)

\(=-10\sqrt{3}\)

b) \(3\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}-\sqrt{4+2\sqrt{3}}\)

\(=3\left|\sqrt{2}-\sqrt{3}\right|-\sqrt{\left(\sqrt{3}+1\right)^2}\)

\(=3\left(\sqrt{3}-\sqrt{2}\right)-\left|\sqrt{3}+1\right|\)

\(=3\sqrt{3}-3\sqrt{2}-\sqrt{3}-1\)

\(=2\sqrt{3}-3\sqrt{2}-1\)

c) \(\left(\frac{2x+1}{x\sqrt{x}-1}-\frac{\sqrt{x}}{x+\sqrt{x}+1}\right)\div\frac{1}{x-2\sqrt{x}+1}\)

\(=\frac{2x+1-\left(\sqrt{x}-1\right)\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\div\frac{1}{\left(\sqrt{x}-1\right)^2}\)

\(=\frac{2x+1-x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\left(\sqrt{x}-1\right)^2\)

\(=\frac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\left(\sqrt{x}-1\right)^2\)

\(=\sqrt{x}-1\)

Đúng(0)

Vũ Khánh Linh

25 tháng 7 2018

P = ( \(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2}{x-4}\)) : ( \(\sqrt{x}-1+\dfrac{\sqrt{x}-4}{\sqrt{x}}\)) Với x > 0 ; x khác 4

a) Chứng minh P = \(\sqrt{x}+3\)

b) Tìm x sao cho P = x + 3

#Hỏi cộng đồng OLM #Toán lớp 9

Phùng Khánh Linh

27 tháng 7 2018

\(a.P=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2}{x-4}\right).\left(\sqrt{x}-1+\dfrac{\sqrt{x}-4}{\sqrt{x}}\right)=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{x-4}{\sqrt{x}}=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x-4}.\dfrac{x-4}{\sqrt{x}}=\sqrt{x}+3\left(x>0;x\ne4\right)\)

\(b.P=x+3\) ⇔ \(\sqrt{x}+3=x+3\Leftrightarrow\sqrt{x}\left(\sqrt{x}-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(KTM\right)\\x=1\left(TM\right)\end{matrix}\right.\)

KL........

Đúng(0)

Đan Linh

27 tháng 10 2017

giải phương trình

a)\(\dfrac{\sqrt{x}-2}{\sqrt{x}-4}=\dfrac{\sqrt{x}-6}{\sqrt{x}-7}\)

b)\(2+\sqrt[3]{x+5}=0\)

c)0,5\(\sqrt{\dfrac{2}{x}}-\sqrt{\dfrac{8}{25x}}+\sqrt{\dfrac{1}{4x}}=\dfrac{1}{5}\)

#Hỏi cộng đồng OLM #Toán lớp 9

Phan Anh Thư

28 tháng 10 2017

\(< =>\sqrt[3]{x+5}=-2\)
<=> \(\left(\sqrt[3]{x+5}\right)^3=-8\)
<=> \(x+5=-8\)
<=> x=-13

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP