K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
1 tháng 7 2015
\(ax+2x+ay+2y+4=x\left(a+2\right)+y\left(a+2\right)+4=\left(a+2\right)\left(x+y\right)+4=\left(a+2\right)\left(a-2\right)+4=a^2-4+4=a^2\)
từ a-2=x+y => y=a-2-x
13 tháng 8 2017
bn post nhiều nên mình ghi đáp án thôi nhé phần nào sai đề mình cho qua
b)\(\left(x+1\right)\left(xy+1\right)\)
c)\(\left(a+b\right)\left(x+y\right)\)
d)\(\left(x-a\right)\left(x-b\right)\)
e)\(\left(x+y\right)\left(xy-1\right)\)
f)\(\left(a-b\right)\left(x^2+y\right)\)
TN
19 tháng 8 2017
\(a,7x^2-7xy-4x+4y\)
\(=7x\left(x-y\right)-4\left(x-y\right)\)
\(=\left(7x-4\right)\left(x-y\right)\)
\(b,2x-2y+ax-ay\)
\(=2\left(x-y\right)+a\left(x-y\right)\)
\(=\left(a+2\right)\left(x-y\right)\)
\(c,x^2-x-y^2-y\)
\(=\left(x^2-y^2\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y\right)-\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-1\right)\)
\(d,ax+ay-2x-2y\)
\(=a\left(x+y\right)-2\left(x+y\right)\)
\(=\left(a-2\right)\left(x+y\right)\)
\(e,x\left(a+b\right)-a-b=x\left(a+b\right)-\left(a+b\right)\)
\(=\left(x-1\right)\left(a+b\right)\)
LK
2 tháng 7 2018
1) x - y - a(x - y) = (x - y) - a(x - y) = (1 - x)(x - y)
2) a - b + x(a - b) = (a - b) + x(a - b) = (1 + x)(a - b)
3) a(x - y) - x + y = a(x - y) - (x - y) = (a - 1)(x - y)
4) x(a - b) - a + b = x(a - b) - (a - b) = (x - 1)(a - b)
5) ax + ay + bx + by = a(x + y) + b(x + y) = (a + b)(x + y)
6) ax + ay - bx - by = a(x + y) - b(x + y) = (a - b)(x + y)
7) - 2x - 2y + ax + ay = -2(x + y) + a(x + y) = (a - 2)(x + y)
8) x2 - xy - 2x + 2y = x(x - y) - 2(x - y) = (x - 2)(x - y)
Sorry nha, giờ mình chỉ rảnh làm 8 câu thôi
19 tháng 8 2021
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
14 tháng 8 2015
a) TA có :
\(\left(x^2+cx+2\right)\left(ax+b\right)=ax^3+bx^2+acx^2+bcx+2ax+2b\)
\(=ax^3+x^2\left(b+ac\right)+x\left(bc+2a\right)+2b\) = \(=x^3-x^2-2\)
=> a = 1
=>\(2b=-2\Rightarrow b=-1\)
=> b + ac = -1 => -1 + 1.c = -1 => -1 + c = -1 => c = -1 + 1 = 0
VẬy a = 1 ; b = -1 ; c = 0
PT
0
KB
11 tháng 9 2018
1 ) Ta có :
\(ax+2x+ay+2y+4\)
\(=x\left(a+2\right)+y\left(a+2\right)+4\)
\(=\left(x+y\right)\left(a+2\right)+4\)
\(=\left(a-2\right)\left(a+2\right)+4\) ( do \(x+y=a-2\) )
\(=a^2-4+4\)
\(=a^2\left(đpcm\right)\)
2 ) \(\left(ax+b\right)\left(x^2-x-1\right)=ax^3+cx^2-1\)
\(\Leftrightarrow ax^3+bx^2-ax^2-bx-ax-b=ax^3+cx^2-1\)
\(\Leftrightarrow ax^3+x^2\left(b-a\right)-\left(b+a\right)x-b=ax^3+x^2c-0.x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}b-a=c\\b+a=0\\b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-a=c\\1+a=0\\b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-a=c\\a=-1\\b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=2\\a=-1\\b=1\end{matrix}\right.\)
Vậy \(a=-1;b=1;c=2\)
PT
11 tháng 9 2018
Ta có:
\(ax+2x+ay+2y+4\)
\(=\left(ax+ay\right)+\left(2x+2y\right)+4\)
\(=a\left(x+y\right)+2\left(x+y\right)+4\)
\(=\left(x+y\right)\left(a+2\right)+4\)
Thay \(x+y=a-2\), ta được
\(=\left(a-2\right)\left(a+2\right)+4\)
\(=a^2-4+4\)
\(=a^2\)
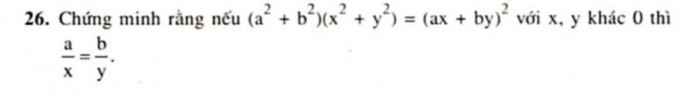
\(VT=ax+2x+ay+2y+4\)
\(=a\left(x+y\right)+2\left(x+y\right)+4\)
\(=a\left(a-2\right)+2\left(a-2\right)+4\)
\(=a^2-2a+2a-4+4=a^2=VP\)
Ta có: \(VT=ax+2x+ay+2y+4\)
\(=\left(c+y\right)a+2\left(x+y\right)+4\)
\(=\left(a+2\right)\left(x+y\right)+4\)
mà \(a-2=x+y\)
\(\Rightarrow VT=\left(a+2\right)\left(a-2\right)=a^2-4+4=a^2\)
\(\Leftrightarrow VP\) -> ĐPCM.